
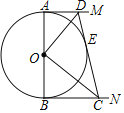
【题目】⊙O直径AB=12cm,AM和BN是⊙O的切线,DC切⊙O于点E且交AM于点D,交BN于点C,设AD=x,BC=y.
(1)求y与x之间的关系式;
(2)x,y是关于t的一元二次方程2t2﹣30t+m=0的两个根,求x,y的值;
(3)在(2)的条件下,求△COD的面积.
【答案】(1)y=![]() ;(2)
;(2)![]() 或
或![]() ;(3)45.
;(3)45.
【解析】
(1)如图,作DF⊥BN交BC于F,根据切线长定理得![]() ,则DC=DE+CE=x+y,在
,则DC=DE+CE=x+y,在![]() 中根据勾股定理,就可以求出y与x之间的关系式.
中根据勾股定理,就可以求出y与x之间的关系式.
(2)由(1)求得![]() ,由根与系数的关系求得
,由根与系数的关系求得![]() 的值,通过解一元二次方程即可求得x,y的值.
的值,通过解一元二次方程即可求得x,y的值.
(3)如图,连接OD,OE,OC,由AM和BN是⊙O的切线,DC切⊙O于点E,得到![]() ,
,![]() ,
,![]() ,推出S△AOD=S△ODE,S△OBC=S△COE,即可得出答案.
,推出S△AOD=S△ODE,S△OBC=S△COE,即可得出答案.
(1)如图,作DF⊥BN交BC于F;
∵AM、BN与⊙O切于点定A、B,
∴AB⊥AM,AB⊥BN.
又∵DF⊥BN,
∴∠BAD=∠ABC=∠BFD=90°,
∴四边形ABFD是矩形,
∴BF=AD=x,DF=AB=12,
∵BC=y,
∴FC=BC﹣BF=y﹣x;
∵DE切⊙O于E,
∴DE=DA=xCE=CB=y,
则DC=DE+CE=x+y,
在Rt△DFC中,
由勾股定理得:(x+y)2=(y﹣x)2+122,
整理为:y=![]() ,
,
∴y与x的函数关系式是y=![]() .
.
(2)由(1)知xy=36,
x,y是方程2x2﹣30x+a=0的两个根,
∴根据韦达定理知,xy=![]() ,即a=72;
,即a=72;
∴原方程为x2﹣15x+36=0,
解得![]() 或
或![]() .
.
(3)如图,连接OD,OE,OC,
∵AD,BC,CD是⊙O的切线,
∴OE⊥CD,AD=DE,BC=CE,
∴S△AOD=S△ODE,
S△OBC=S△COE,
∴S△COD=![]() ×
×![]() ×(3+12)×12=45.
×(3+12)×12=45.


科目:初中数学 来源: 题型:
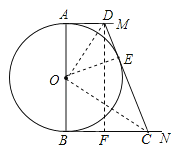
【题目】如图,四边形ABCD中,AB=AD,∠BAD=60°,∠BCD=30°,将AC绕着点A顺时针旋转60°得AE,连接BE,CE.
(1)求证:△ADC≌△ABE;
(2)求证:![]()
(3)若AB=2,点Q在四边形ABCD内部运动,且满足![]() ,直接写出点Q运动路径的长度.
,直接写出点Q运动路径的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+2x+3.
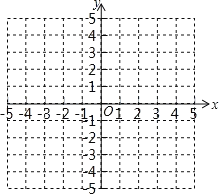
(1)求函数图象的顶点坐标,并画出这个函数的图象;
(2)根据图象,直接写出:
①当函数值y>0时,自变量x的取值范围;
②当2<x<2时,函数值y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AE、BE是△ABC的两个内角的平分线,过点A作AD⊥AE.交BE的延长线于点D.若AD=AB,BE:ED=1:2,则cos∠ABC=_____.
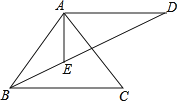
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x﹣1与抛物线y=﹣x2+6x﹣5相交于A、D两点.抛物线的顶点为C,连结AC.
(1)求A,D两点的坐标;
(2)点P为该抛物线上一动点(与点A、D不重合),连接PA、PD.
①当点P的横坐标为2时,求△PAD的面积;
②当∠PDA=∠CAD时,直接写出点P的坐标.
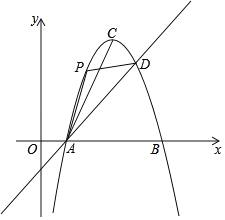
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.任意给定一个正方形,一定存在另一个正方形,它的周长和面积分别是已知正方形周长和面积的一半
B.任意给定一个正方形,一定存在另一个正方形,它的周长和面积分别是已知正方形周长和面积的2倍
C.任意给定一个矩形,一定存在另一个矩形,它的周长和面积分别是已知矩形周长和面积的一半
D.任意给定一个矩形,一定存在另一个矩形,它的周长和面积分别是已知矩形周长和面积的2倍
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平,再一次折叠纸片,使点A落在EF上的点A′处,并使折痕经过点B,得到折痕BM,若矩形纸片的宽AB=4,则折痕BM的长为( )
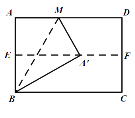
A.![]() B.
B.![]() C.8D.
C.8D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接![]() 年中、日、韩三国青少年橄榄球比赛,南雅中学计划对面积为
年中、日、韩三国青少年橄榄球比赛,南雅中学计划对面积为![]() 运动场进行塑胶改造.经投标,由甲、乙两个工程队来完成,已知甲队每天能改造的面积是乙队每天能改造面积的
运动场进行塑胶改造.经投标,由甲、乙两个工程队来完成,已知甲队每天能改造的面积是乙队每天能改造面积的![]() 倍,并且在独立完成面积为
倍,并且在独立完成面积为![]() 的改造时,甲队比乙队少用
的改造时,甲队比乙队少用![]() 天.
天.
(1)求甲、乙两工程队每天能完成塑胶改造的面积;
(2)设甲工程队施工![]() 天,乙工程队施工
天,乙工程队施工![]() 天,刚好完成改造任务,求
天,刚好完成改造任务,求![]() 与
与![]() 的函数解析式;
的函数解析式;
(3)若甲队每天改造费用是![]() 万元,乙队每天改造费用是
万元,乙队每天改造费用是![]() 万元,且甲、乙两队施工的总天数不超过
万元,且甲、乙两队施工的总天数不超过![]() 天,如何安排甲、乙两队施工的天数,使施工总费用最低?并求出最低的费用.
天,如何安排甲、乙两队施工的天数,使施工总费用最低?并求出最低的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.Rt△ABC中,已知∠C=90°,∠B=50°,点D在边BC上,BD=2CD(图4).把△ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m=_________![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com