
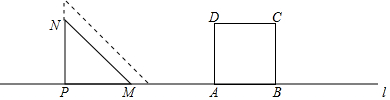
分析 (1)根据平移的性质、三角形的面积公式计算即可;
(2)分斜边MN经过点A、点B、D、点C三种情况,列方程计算即可.
解答 解:(1)等腰直角△PMN的直角边长为3+2t,
面积为:$\frac{1}{2}$(3+2t)2,
故答案为:3+2t;$\frac{1}{2}$(3+2t)2;
(2)当斜边MN经过点A时,3+2t=7+t,
解得,t=4,
斜边MN恰好经过B、D时,3+2t=7+t+3,
解得,t=7,
斜边MN经过得C时,3+2t=7+t+3+3,
解得,t=10,
则t=4s或7s或10s时,△PMN的斜边MN恰好经过正方形ABCD的顶点.
点评 本题考查的是正方形的性质、等腰直角三角形的性质、平移的性质,掌握平移的性质:新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等是解题的关键.


科目:初中数学 来源: 题型:解答题
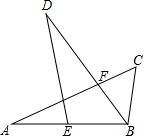 如图,已知△ABC≌△DEB,点E在AB上,AC与BD交于点F,AB=6,BC=3,∠C=55°,∠D=25°.
如图,已知△ABC≌△DEB,点E在AB上,AC与BD交于点F,AB=6,BC=3,∠C=55°,∠D=25°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
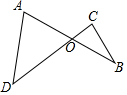 阅读下题及一位同学的解答过程:如图,AB和CD相交于点O,且OA=OB,∠A=∠C,那么△AOD与△COB全等吗?若全等,试写出证明过程,若不全等,请说明理由
阅读下题及一位同学的解答过程:如图,AB和CD相交于点O,且OA=OB,∠A=∠C,那么△AOD与△COB全等吗?若全等,试写出证明过程,若不全等,请说明理由查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com