
【题目】已知函数y=ax2+bx+c(a≠0)的图象与函数y=x-![]() 的图象如图所示,则下列结论:①ab>0;②c>-
的图象如图所示,则下列结论:①ab>0;②c>-![]() ;③a+b+c<-
;③a+b+c<-![]() ;④方程ax2+(b-1)x+c+
;④方程ax2+(b-1)x+c+![]() =0有两个不相等的实数根.其中正确的有( )
=0有两个不相等的实数根.其中正确的有( )
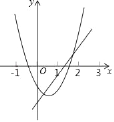
A. 4个 B. 3个 C. 2个 D. 1个
【答案】B
【解析】
根据抛物线的开口方向及对称轴的位置确定a、b的符号,即可判定①;根据抛物线与y轴的交点在直线y=x﹣![]() 与y轴交点的上方,即可判定②;观察图象可得当x=1时,ax2+bx+c<x﹣
与y轴交点的上方,即可判定②;观察图象可得当x=1时,ax2+bx+c<x﹣![]() ,即可判定③;由函数y=ax2+bx+c(a≠0)的图象与函数y=x﹣
,即可判定③;由函数y=ax2+bx+c(a≠0)的图象与函数y=x﹣![]() 的图象有两个不同的交点,即可判定④.
的图象有两个不同的交点,即可判定④.
∵抛物线开口朝上,
∴a>0,
∵对称轴x=﹣![]() 在y轴的右侧,
在y轴的右侧,
∴b<0,
∴ab<0,故①错误;
∵抛物线与y轴的交点在直线y=x﹣![]() 与y轴交点的上方,
与y轴交点的上方,
∴c>﹣![]() ,故②正确;
,故②正确;
观察图象可得,当x=1时,ax2+bx+c<x﹣![]() ,即a+b+c<﹣
,即a+b+c<﹣![]() ;故③正确;
;故③正确;
∵函数y=ax2+bx+c(a≠0)的图象与函数y=x﹣![]() 的图象有两个不同的交点,
的图象有两个不同的交点,
∴ax2+(b﹣1)x+c+![]() =0有两个不相等的实数根,故④正确.
=0有两个不相等的实数根,故④正确.
故选B.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两名战士在相同条件下各射击10次,每次命中的环数如下:
甲:8,6,7,8,9,10,6,5,4,7
乙:7,9,8,5,6,7,7,6,7,8
(1)分别计算以上两组数据的平均数;
(2)分别计算以上两组数据的方差.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B.
(1)求一次函数的解析式;
(2)判断点C(4,-2)是否在该一次函数的图象上,说明理由;
(3)若该一次函数的图象与x轴交于D点,求△BOD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域,其中标有数字“1”的扇形圆心角为120°.转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止)
(1)转动转盘一次,求转出的数字是-2的概率;
(2)转动转盘两次,用树状图或列表法求这两次分别转出的数字之积为正数的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展“数学史”知识竞赛活动,八年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.
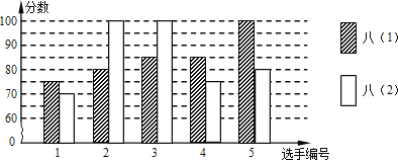
(1)请计算八(1)班、八(2)班两个班选出的5名选手复赛的平均成绩;
(2)请判断哪个班选出的5名选手的复赛成绩比较稳定,并说明理由?
查看答案和解析>>
科目:初中数学 来源: 题型:
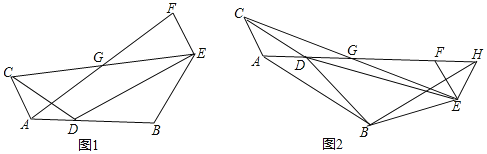
【题目】已知如图,△ADC和△BDE均为等腰三角形,∠CAD=∠DBE,AC=AD,BD=BE,连接CE,点G为CE的中点,过点E作AC的平行线与线段AG延长线交于点F.
(1)当A,D,B三点在同一直线上时(如图1),求证:G为AF的中点;
(2)将图1中△BDE绕点D旋转到图2位置时,点A,D,G,F在同一直线上,点H在线段AF的延长线上,且EF=EH,连接AB,BH,试判断△ABH的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
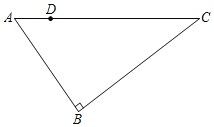
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,点D为AC边上的个动点,点D从点A出发,沿边AC向C运动,当运动到点C时停止,设点D运动时间为t秒,点D运动的速度为每秒1个单位长度的.
(1)当t=2时,求CD的长;
(2)求当t为何值时,线段BD最短?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂,甲负责加工A型零件,乙负责加工B型零件.已知甲加工60个A型零件所用时间和乙加工80个B型零件所用时间相同,每天甲、乙两人共加工两种零件35个.
(1)求甲、乙每天各加工多少个零件;
(2)根据市场预测估计,加工一个A型零件所获得的利润为35元/件,加工一个B型零件所获得的利润每件比A型少5元,现在需要加工甲、乙两种零件共300个且要求所获得的总利润不低于9850元,求至少应该生产多少个A型零件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com