
 如图,点M是直线y=2x+3在第二象限上的动点,过点M作MN垂直x轴于点N,在y轴的正半轴上求点P,使△MNP为等腰直角三角形,请写出符合条件的点P的坐标(0,0)、(0,1)或(0,$\frac{3}{4}$).
如图,点M是直线y=2x+3在第二象限上的动点,过点M作MN垂直x轴于点N,在y轴的正半轴上求点P,使△MNP为等腰直角三角形,请写出符合条件的点P的坐标(0,0)、(0,1)或(0,$\frac{3}{4}$). 分析 设点M的坐标为(m,2m+3),由点M在第二象限且在直线y=2x+3上,利用一次函数图象上点的坐标特征即可得出m的取值范围,分∠MNP=90°、∠NMP=90°以及∠MPN=90°三种情况考虑,利用等腰直角三角形的性质找出点M的坐标,将其代入一次函数解析式中求出m值,由此即可得出点P的坐标.
解答 解:设点M的坐标为(m,2m+3),
令y=2x+3>0,解得:x>-$\frac{3}{2}$,
∴-$\frac{3}{2}$<x<0.
当∠MNP=90°时,MN=ON,
∴点M的坐标为(m,-m),
∵点M在直线y=2x+3上,
∴-m=2m+3,
解得:m=-1,
∴点P的坐标为(0,0);
当∠NMP=90°时,MN=PM,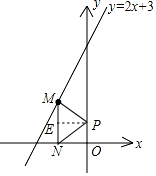
∴点M的坐标为(m,-m),
∵点M在直线y=2x+3上,
∴-m=2m+3,
解得:m=-1,
∴点P的坐标为(0,1);
当∠MPN=90°时,过点P作PE⊥MN于点E,
∵△MNP为等腰直角三角形,
∴MN=2PE,
∴点M的坐标为(m,-2m),
∵点M在直线y=2x+3上,
∴-2m=2m+3,
解得:m=-$\frac{3}{4}$,
∴点P的坐标为(0,$\frac{3}{4}$).
综上可知:符合条件的点P的坐标为(0,0)、(0,1)或(0,$\frac{3}{4}$).
点评 本题考查了一次函数图象上点的坐标特征以及等腰直角三角形的性质,分∠MNP=90°、∠NMP=90°以及∠MPN=90°三种情况考虑是解题的关键.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知,如图,在⊙O中,直径AB=4,点E是OA上任意一点,过点E作弦CD⊥AB,点F是弧AB上的一点,连接AF交CE于点H,连结AC,CF,BD.
已知,如图,在⊙O中,直径AB=4,点E是OA上任意一点,过点E作弦CD⊥AB,点F是弧AB上的一点,连接AF交CE于点H,连结AC,CF,BD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3500(1+x)=4200 | B. | 3500(1-x)+3500(1-x)2=4200 | ||
| C. | 3500(1-x)=4200 | D. | 3500(1-x)2=4200 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -16x-$\frac{1}{2}$ | B. | -16x+$\frac{1}{2}$ | C. | -16x-8 | D. | -16x+8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com