
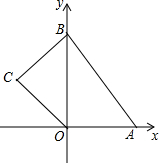
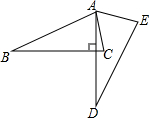
 ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ĖıߊĪOABCµÄ¶„µćOŹĒ×ų±źŌµć£¬µćAµÄ×ų±źĪŖ£Ø6£¬0£©£¬µćBµÄ×ų±źĪŖ£Ø0£¬8£©£¬µćCµÄ×ų±źĪŖ£Ø-2$\sqrt{5}$£¬4£©£¬µćM£¬N·Ö±šĪŖĖıߊĪOABC±ßÉĻµÄ¶Æµć£¬¶ÆµćM“ÓµćOæŖŹ¼£¬ŅŌĆæĆė1øöµ„Ī»³¤¶ČµÄĖŁ¶ČŃŲO”śA”śBĀ·ĻßĻņÖŠµćBŌČĖŁŌĖ¶Æ£¬¶ÆµćN“ÓOµćæŖŹ¼£¬ŅŌĆæĆėĮ½øöµ„Ī»³¤¶ČµÄĖŁ¶ČŃŲO”śC”śB”śAĀ·ĻßĻņÖÕµćAŌČĖŁŌĖ¶Æ£¬µćM£¬NĶ¬Ź±“ÓOµć³ö·¢£¬µ±ĘäÖŠŅ»µćµ½“ļÖÕµćŗó£¬ĮķŅ»µćŅ²ĖęÖ®Ķ£Ö¹ŌĖ¶Æ£¬Éč¶ÆµćŌĖ¶ÆµÄŹ±¼ätĆė£Øt£¾0£©£¬”÷OMNµÄĆ껿ĪŖS£®
ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ĖıߊĪOABCµÄ¶„µćOŹĒ×ų±źŌµć£¬µćAµÄ×ų±źĪŖ£Ø6£¬0£©£¬µćBµÄ×ų±źĪŖ£Ø0£¬8£©£¬µćCµÄ×ų±źĪŖ£Ø-2$\sqrt{5}$£¬4£©£¬µćM£¬N·Ö±šĪŖĖıߊĪOABC±ßÉĻµÄ¶Æµć£¬¶ÆµćM“ÓµćOæŖŹ¼£¬ŅŌĆæĆė1øöµ„Ī»³¤¶ČµÄĖŁ¶ČŃŲO”śA”śBĀ·ĻßĻņÖŠµćBŌČĖŁŌĖ¶Æ£¬¶ÆµćN“ÓOµćæŖŹ¼£¬ŅŌĆæĆėĮ½øöµ„Ī»³¤¶ČµÄĖŁ¶ČŃŲO”śC”śB”śAĀ·ĻßĻņÖÕµćAŌČĖŁŌĖ¶Æ£¬µćM£¬NĶ¬Ź±“ÓOµć³ö·¢£¬µ±ĘäÖŠŅ»µćµ½“ļÖÕµćŗó£¬ĮķŅ»µćŅ²ĖęÖ®Ķ£Ö¹ŌĖ¶Æ£¬Éč¶ÆµćŌĖ¶ÆµÄŹ±¼ätĆė£Øt£¾0£©£¬”÷OMNµÄĆ껿ĪŖS£®·ÖĪö £Ø1£©ĄūÓĆ¹“¹É¶ØĄķ¼“æɽā¾öĪŹĢā£»
£Ø2£©ČēĶ¼1ÖŠ£¬×÷CE”ĶxÖįÓŚE£®Į¬½ÓCM£®µ±t=3Ź±£¬µćNÓėCÖŲŗĻ£¬OM=3£¬Ņ×Ēó”÷OMNµÄĆ껿£»
£Ø3£©ČēĶ¼2ÖŠ£¬µ±3£¼t£¼6Ź±£¬µćNŌŚĻ߶ĪBCÉĻ£¬BN=12-2t£¬×÷NG”ĶOBÓŚG£¬CF”ĶOBÓŚF£®ŌņF£Ø0£¬4£©£®ÓÉGN”ĪCF£¬ĶĘ³ö$\frac{BN}{BC}$=$\frac{BG}{BF}$£¬¼“$\frac{12-2t}{6}$=$\frac{BG}{4}$£¬æɵĆBG=8-$\frac{4}{3}$t£¬ÓÉ“Ė¼“æɽā¾öĪŹĢā£»
£Ø4£©·ÖČżÖÖĒéŠĪ¢Łµ±µćNŌŚ±ß³¤ÉĻ£¬µćMŌŚOAÉĻŹ±£®¢ŚČēĶ¼3ÖŠ£¬µ±M”¢NŌŚĻ߶ĪABÉĻ£¬ĻąÓöÖ®Ē°£®×÷OE”ĶABÓŚE£¬ŌņOE=$\frac{OB•OA}{AB}$=$\frac{24}{5}$£¬ĮŠ³ö·½³Ģ¼“æɽā¾öĪŹĢā£®¢ŪĶ¬·Øµ±M”¢NŌŚĻ߶ĪABÉĻ£¬ĻąÓöÖ®ŗó£¬ĮŠ³ö·½³Ģ¼“æÉ£»
½ā“š ½ā£ŗ£Ø1£©ŌŚRt”÷AOBÖŠ£¬”ß”ĻAOB=90”ć£¬OA=6£¬OB=8£¬
”ąAB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10£®
BC=$\sqrt{£Ø2\sqrt{5}£©^{2}+{4}^{2}}$=6£¬
¹Ź“š°øĪŖ10£¬6£®
£Ø2£©ČēĶ¼1ÖŠ£¬×÷CE”ĶxÖįÓŚE£®Į¬½ÓCM£®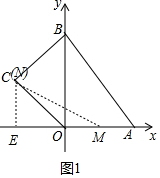
”ßC£Ø-2$\sqrt{5}$£¬4£©£¬
”ąCE=4OE=2$\sqrt{5}$£¬
ŌŚRt”÷COEÖŠ£¬OC=$\sqrt{O{E}^{2}+C{E}^{2}}$=$\sqrt{£Ø2\sqrt{5}£©^{2}+{4}^{2}}$=6£¬
µ±t=3Ź±£¬µćNÓėCÖŲŗĻ£¬OM=3£¬
”ąS”÷ONM=$\frac{1}{2}$•OM•CE=$\frac{1}{2}$”Į3”Į4=6£¬
¼“S=6£®
£Ø3£©ČēĶ¼2ÖŠ£¬µ±3£¼t£¼6Ź±£¬µćNŌŚĻ߶ĪBCÉĻ£¬BN=12-2t£¬×÷NG”ĶOBÓŚG£¬CF”ĶOBÓŚF£®ŌņF£Ø0£¬4£©£®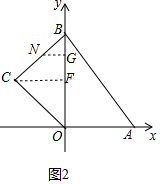
”ßOF=4£¬OB=8£¬
”ąBF=8-4=4£¬
”ßGN”ĪCF£¬
”ą$\frac{BN}{BC}$=$\frac{BG}{BF}$£¬¼“$\frac{12-2t}{6}$=$\frac{BG}{4}$£¬
”ąBG=8-$\frac{4}{3}$t£¬
”ąy=OB-BG=8-£Ø8-$\frac{4}{3}$t£©=$\frac{4}{3}$t£®
£Ø4£©¢Łµ±µćNŌŚ±ß³¤ÉĻ£¬µćMŌŚOAÉĻŹ±£¬$\frac{1}{2}$•$\frac{4}{3}$t•t=$\frac{48}{5}$£¬
½āµĆt=$\frac{6\sqrt{10}}{5}$£ØøŗøłŅŃ¾ÉįĘś£©£®
¢ŚČēĶ¼3ÖŠ£¬µ±M”¢NŌŚĻ߶ĪABÉĻ£¬ĻąÓöÖ®Ē°£®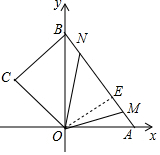
×÷OE”ĶABÓŚE£¬ŌņOE=$\frac{OB•OA}{AB}$=$\frac{24}{5}$£¬
ÓÉĢāŅā$\frac{1}{2}$[10-£Ø2t-12£©-£Øt-6£©]•$\frac{24}{5}$=$\frac{48}{5}$£¬
½āµĆt=8£¬
Ķ¬·Øµ±M”¢NŌŚĻ߶ĪABÉĻ£¬ĻąÓöÖ®ŗó£®
ÓÉĢāŅā$\frac{1}{2}$•[£Ø2t-12£©+£Øt-6£©-10]•$\frac{24}{5}$=$\frac{48}{5}$£¬
½āµĆt=$\frac{32}{3}$£¬
×ŪÉĻĖłŹö£¬ČōS=$\frac{48}{5}$£¬“ĖŹ±tµÄÖµ8s»ņ$\frac{32}{3}$s»ņ$\frac{6\sqrt{10}}{5}$s£®
µćĘĄ ±¾Ģāæ¼²éĖıߊĪ×ŪŗĻĢā”¢Ę½ŠŠĻß·ÖĻ߶Ī°É³É±ČĄż¶ØĄķ”¢¹“¹É¶ØĄķ”¢½āÖ±½ĒČż½ĒŠĪµČÖŖŹ¶£¬½āĢāµÄ¹Ų¼üŹĒĮé»īŌĖÓĆĖłŃ§ÖŖŹ¶½ā¾öĪŹĢā£¬Ń§»įÓĆ·ÖĄąĢÖĀŪµÄĖ¼ĻėĖ¼æ¼ĪŹĢā£¬ŹōÓŚÖŠæ¼Ń¹ÖįĢā£®


 ³õ֊ѧŅµæ¼ŹŌµ¼ÓėĮ·ĻµĮŠ“š°ø
³õ֊ѧŅµæ¼ŹŌµ¼ÓėĮ·ĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
 ČēĶ¼£¬½«”÷ABCČʵćAÄꏱÕėŠż×ŖŅ»¶Ø½Ē¶Č£¬µĆµ½”÷ADE£®ČōAD”ĶBC£¬”ĻCAE=65”ć£¬”ĻE=70”ć£¬Ōņ”ĻBACµÄ“óŠ”ĪŖ85¶Č£®
ČēĶ¼£¬½«”÷ABCČʵćAÄꏱÕėŠż×ŖŅ»¶Ø½Ē¶Č£¬µĆµ½”÷ADE£®ČōAD”ĶBC£¬”ĻCAE=65”ć£¬”ĻE=70”ć£¬Ōņ”ĻBACµÄ“óŠ”ĪŖ85¶Č£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | $\frac{1}{4}$ | B£® | -$\frac{1}{4}$ | C£® | ”Ą$\frac{1}{4}$ | D£® | ”Ą$\frac{1}{2}$ |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
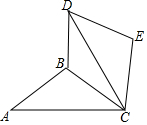 ČēĶ¼£¬”÷ABCÖŠ£¬AB=BC=5£¬AC=8£¬½«”÷ABCČʵćCĖ³Ź±Õė·½ĻņŠż×Ŗ60”ćµĆµ½”÷DEC£¬Į¬½ÓBD£¬ŌņBDµÄ³¤¶ČĪŖ4$\sqrt{3}$-3£®
ČēĶ¼£¬”÷ABCÖŠ£¬AB=BC=5£¬AC=8£¬½«”÷ABCČʵćCĖ³Ź±Õė·½ĻņŠż×Ŗ60”ćµĆµ½”÷DEC£¬Į¬½ÓBD£¬ŌņBDµÄ³¤¶ČĪŖ4$\sqrt{3}$-3£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
 ČēĶ¼£¬ABŹĒ”ŃOµÄÖ±¾¶£¬AC£¬BC·Ö±šÓė”ŃOĻą½»ÓŚµćD£¬E£¬Į¬½ÓDE£¬ĻÖøų³öĮ½øöĆüĢā£ŗ
ČēĶ¼£¬ABŹĒ”ŃOµÄÖ±¾¶£¬AC£¬BC·Ö±šÓė”ŃOĻą½»ÓŚµćD£¬E£¬Į¬½ÓDE£¬ĻÖøų³öĮ½øöĆüĢā£ŗ| A£® | ¢ŁŹĒÕęĆüĢā ¢ŚŹĒ¼ŁĆüĢā | B£® | ¢ŁŹĒ¼ŁĆüĢā ¢ŚŹĒÕęĆüĢā | ||
| C£® | ¢ŁŹĒ¼ŁĆüĢā ¢ŚŹĒ¼ŁĆüĢā | D£® | ¢ŁŹĒÕęĆüĢā ¢ŚŹĒÕęĆüĢā |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com