
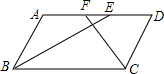
 已知:如图,平行四边形ABCD中,BE平分∠ABC交AD于E,CF平分∠BCD交AD于F,若AB=3,BC=5,则EF=1.
已知:如图,平行四边形ABCD中,BE平分∠ABC交AD于E,CF平分∠BCD交AD于F,若AB=3,BC=5,则EF=1.  中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:选择题
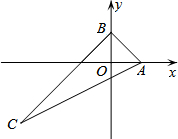 如图,△ABC在平面直角坐标系中,点A、B分别在x轴和y轴上,且OA=OB,边AC所在直线解析式为y=$\frac{1}{2}$x-$\frac{1}{2}$,若△ABC的内心在y轴上,则tan∠ACB的值为( )
如图,△ABC在平面直角坐标系中,点A、B分别在x轴和y轴上,且OA=OB,边AC所在直线解析式为y=$\frac{1}{2}$x-$\frac{1}{2}$,若△ABC的内心在y轴上,则tan∠ACB的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
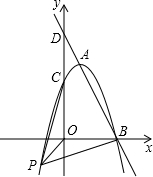 如图,已知直线y=kx+6与抛物线y=ax2+bx+c相交于A,B两点,且点A(1,4)为抛物线的顶点,点B在x轴上.
如图,已知直线y=kx+6与抛物线y=ax2+bx+c相交于A,B两点,且点A(1,4)为抛物线的顶点,点B在x轴上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)解不等式$\left\{\begin{array}{l}{2x+1>-3}\\{\frac{x+3}{5}≤\frac{2x-5}{3}+1}\end{array}\right.$并把不等式组的解集在数轴上表示.
(1)解不等式$\left\{\begin{array}{l}{2x+1>-3}\\{\frac{x+3}{5}≤\frac{2x-5}{3}+1}\end{array}\right.$并把不等式组的解集在数轴上表示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
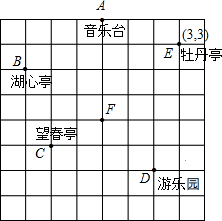 多多和爸爸、妈妈周末到公园游玩,回到家后,他利用平面直角坐标系画出了公园的景区地图,如图所示.可是他忘记了在图中标出原点和x轴、y轴.只知道牡丹园的坐标为(3,3),请你帮他建立平面直角坐标系(画在图中)并求出其它各景点的坐标?
多多和爸爸、妈妈周末到公园游玩,回到家后,他利用平面直角坐标系画出了公园的景区地图,如图所示.可是他忘记了在图中标出原点和x轴、y轴.只知道牡丹园的坐标为(3,3),请你帮他建立平面直角坐标系(画在图中)并求出其它各景点的坐标?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com