
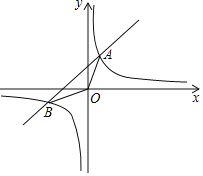
【题目】如图,已知一次函数y=kx+b(k≠0)与反比例函数y=![]() (m≠0)的图象相交于A、B两点,且点A的坐标是(1,2),点B的坐标是(﹣2,w).
(m≠0)的图象相交于A、B两点,且点A的坐标是(1,2),点B的坐标是(﹣2,w).
(1)求一次函数与反比例函数的解析式;
(2)在x轴的正半轴上找一点C,使△AOC的面积等于△ABO的面积,并求出点C的坐标.
【答案】(1)反比例函数的解析式为:y=![]() ,一次函数的解析式为:y=x+1;(2)C(
,一次函数的解析式为:y=x+1;(2)C(![]() ,0).
,0).
【解析】
(1)先根据A(1,2)是反比例函数y=![]() 图象上的点即可得出m的值,进而得出其解析式;把B(-2,w)代入反比例函数的解析式即可得出w的值,进而得出B点坐标,把A、C两点的坐标代入一次函数的解析式即可求出kb的值,进而得出一次函数的解析式
图象上的点即可得出m的值,进而得出其解析式;把B(-2,w)代入反比例函数的解析式即可得出w的值,进而得出B点坐标,把A、C两点的坐标代入一次函数的解析式即可求出kb的值,进而得出一次函数的解析式
(2)根据一次函数的解析式求出D点坐标,由S△ABO=S△AOD+S△BOD得出其面积,再设C(x,0),由三角形的面积公式即可求出x的值解答
(1)∵A(1,2)是反比例函数y=![]() (m≠0)图象上的点,
(m≠0)图象上的点,
∴m=1×2=2,
∴反比例函数的解析式为:y=![]() ,
,
把B(﹣2,w)代入反比例函数y=![]() 得,w=
得,w=![]() =﹣1,
=﹣1,
∴B(﹣2,﹣1),
∵A(1,2),B(﹣2,﹣1)是一次函数y=kx+b图象上的点,
∴![]() ,解得
,解得![]() ,
,
∴一次函数的解析式为:y=x+1;
(2)∵一次函数的解析式为:y=x+1,
∴一次函数与x轴的交点D为(﹣1,0),
∴S△ABO=S△AOD+S△BOD=![]() ×1×2+
×1×2+![]() ×1×1=
×1×1=![]() ,
,
设C(x,0),
∵△AOC的面积等于△ABO的面积,
∴![]() ×2x=
×2x=![]() ,解得x=
,解得x=![]() ,
,
∴C(![]() ,0).
,0).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=BC,∠ABC=90°,D为AC中点,点P是线段AD上的一点,点P与点A、点D不重合),连接BP.将△ABP绕点P按顺时针方向旋转α角(0°<α<180°),得到△A1B1P,连接A1B1、BB1
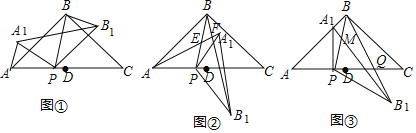
(1)如图①,当0°<α<90°,在α角变化过程中,请证明∠PAA1=∠PBB1.
(2)如图②,直线AA1与直线PB、直线BB1分别交于点E,F.设∠ABP=β,当90°<α<180°时,在α角变化过程中,是否存在△BEF与△AEP全等?若存在,求出α与β之间的数量关系;若不存在,请说明理由;
(3)如图③,当α=90°时,点E、F与点B重合.直线A1B与直线PB相交于点M,直线BB′与AC相交于点Q.若AB=![]() ,设AP=x,CQ=y,求y关于x的函数关系式.
,设AP=x,CQ=y,求y关于x的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于x的一元二次方程![]() (a≠0)有两个不相等的实数根,且其中一个根为另一个根的2倍,那么称这样的方程为“倍根方程”.例如,方程
(a≠0)有两个不相等的实数根,且其中一个根为另一个根的2倍,那么称这样的方程为“倍根方程”.例如,方程![]() 的两个根是2和4,则方程
的两个根是2和4,则方程![]() 就是“倍根方程”.
就是“倍根方程”.
(1)若一元二次方程![]() 是“倍根方程”,则c=
是“倍根方程”,则c=
(2)若方程![]() (a≠0)是倍根方程,且相异两点M(1+t,s),N(4-t,s),都在抛物线
(a≠0)是倍根方程,且相异两点M(1+t,s),N(4-t,s),都在抛物线![]() 上,求一元二次方程
上,求一元二次方程![]() (a≠0)的根.
(a≠0)的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 在抛物线
在抛物线![]() 上,且该抛物线与
上,且该抛物线与![]() 轴分别交于点
轴分别交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
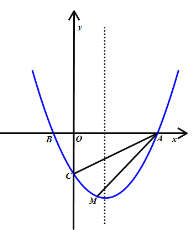
(1)求抛物线的解析式及对称轴;
(2)若点![]() 是抛物线对称轴上的一个动点,求
是抛物线对称轴上的一个动点,求![]() 的最小值;
的最小值;
(3)点![]() 是是抛物线上除点
是是抛物线上除点![]() 外的一点,若
外的一点,若![]() 与
与![]() 的面积相等,求点
的面积相等,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
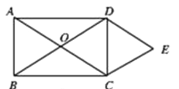
【题目】矩形ABCD的对角线相交于点O.DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若∠ACB=30°,菱形OCED的而积为![]() ,求AC的长.
,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴交于
轴交于![]() 两点
两点
![]() 求抛物线
求抛物线![]() 的解析式;
的解析式;
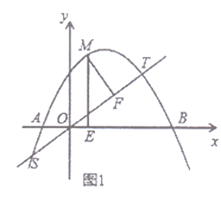
![]() 如图1,直线
如图1,直线![]() 交抛物线
交抛物线![]() 于
于![]() 两点,
两点,![]() 为抛物线
为抛物线![]() 上
上![]() 之间的动点,过
之间的动点,过![]() 点作
点作![]() 轴于点
轴于点![]() 于点
于点![]() ,求
,求![]() 的最大值;
的最大值;
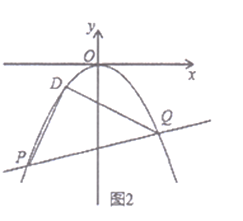
![]() 如图2,平移抛物线
如图2,平移抛物线![]() 的顶点到原点得抛物线
的顶点到原点得抛物线![]() ,直线
,直线![]() 交抛物线
交抛物线![]() 于
于![]() 、
、![]() 两点,在抛物线
两点,在抛物线![]() 上存在一个定点
上存在一个定点![]() ,使
,使![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
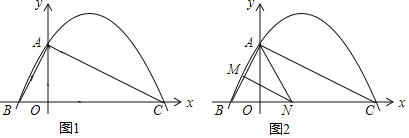
【题目】如图1,已知二次函数y=ax2+![]() x+c(a≠0)的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
x+c(a≠0)的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
(1)请直接写出二次函数y=ax2+![]() x+c的表达式;
x+c的表达式;
(2)判断△ABC的形状,并说明理由;
(3)若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,请写出此时点N的坐标;
(4)如图2,若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求此时点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】面对新冠肺炎疫情对经济运行的冲击,中国人民银行营业管理部(中国人民银行总行在京派驻机构)与相关部门多方动员,合力推动辖内9家全国性银行北京分行和3家地方法人银行为疫情防控重点企业提供优惠利率贷款,有力有序推动企业复工复产.截至2020年4月2日,已发放优惠利率贷款573笔,金额280 亿元.将280 亿元用科学记数法表示应为( )
A.28×![]() 元B.2.8×
元B.2.8×![]() 元C.2.8×
元C.2.8×![]() 元D.2.8×
元D.2.8×![]() 元
元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com