根据下列条件解直角三角形:Rt△ABC中,∠C=90°,BC=5,AB=7.(边长保留根号,角度精确到1°)
解:在Rt△ABC中,BC=5,AB=7,
根据勾股定理得:AC=

=
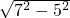
=2

,
∵sinA=

=

,
∴∠A≈46°,
∴∠B=90°-46°=44°.
分析:由BC与AB的长,利用勾股定理求出AC的长,利用锐角三角函数定义求出sinA的值,确定出A的度数,由直角三角形两锐角互余,即可求出B的度数.
点评:此题考查了解直角三角形,涉及的知识有:勾股定理,锐角三角函数定义,以及直角三角形的性质,熟练掌握勾股定理及锐角三角函数定义是解本题的关键.
