
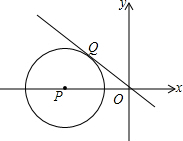
 如图,⊙P是圆心P(-$\sqrt{2}$,0),正比例函数y=-x的图象与⊙P相切于点Q,则Q点的坐标为( )
如图,⊙P是圆心P(-$\sqrt{2}$,0),正比例函数y=-x的图象与⊙P相切于点Q,则Q点的坐标为( )| A. | (-1,1) | B. | ($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$) | C. | (-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$) | D. | ($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$) |
分析 连接PQ,过点Q作QA⊥x轴于A,由正比例函数y=-x的图象与⊙P相切于点Q,得到∠PQO=90°,∠QOP=45°,根据等腰直角三角形的性质即可得到结果.
解答  解:连接PQ,过点Q作QA⊥x轴于A,
解:连接PQ,过点Q作QA⊥x轴于A,
∵正比例函数y=-x的图象与⊙P相切于点Q,
∴∠PQO=90°,∠QOP=45°,
∴QA=OA=$\frac{1}{2}$OP,
∵P(-$\sqrt{2}$,0),
∴OP=$\sqrt{2}$,
∴QA=OA=$\frac{\sqrt{2}}{2}$,
∴Q(-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$)
故选C.
点评 本题考查了切线的性质,正比例函数图象上点的坐标特征,等腰直角三角形的性质,知道y=-x的图象是第二象限角平分线是解题的关键.


科目:初中数学 来源: 题型:选择题
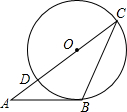 如图,△ABC的边AC与⊙O相交于C,D两点,且经过圆心O,边AB与⊙O相切,切点为B.如果∠A=34°,那么∠C等于( )
如图,△ABC的边AC与⊙O相交于C,D两点,且经过圆心O,边AB与⊙O相切,切点为B.如果∠A=34°,那么∠C等于( )| A. | 28° | B. | 33° | C. | 34° | D. | 56° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 用38m长的竹篱笆建一个矩形养鸡场,养鸡场一面用砖砌成,其它用竹篱笆围成,并且在与砖墙相对的一面开2m的门(门不用篱笆),问怎样围竹篱笆,使得养鸡场占地面积最大?最大面积是多少?
用38m长的竹篱笆建一个矩形养鸡场,养鸡场一面用砖砌成,其它用竹篱笆围成,并且在与砖墙相对的一面开2m的门(门不用篱笆),问怎样围竹篱笆,使得养鸡场占地面积最大?最大面积是多少?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.01×10-6kg | B. | 2.01×10-5kg | C. | 20.1×10-7kg | D. | 20.1×10-6kg |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com