
分析 ①原式利用异号两数相加的法则计算即可得到结果;
②原式利用减法法则变形,计算即可得到结果;
③原式利用减法法则变形,计算即可得到结果;
④原式从左到右依次计算即可得到结果;
⑤原式从左到右依次计算即可得到结果.
解答 解:①原式=10-4=6;
②原式=-23+58+5=-23+63=40;
③原式=1$\frac{3}{4}$+$\frac{1}{4}$-$\frac{5}{6}$-1$\frac{1}{6}$=2-2=0;
④原式=-5×$\frac{3}{2}$×$\frac{3}{2}$×5=$\frac{225}{4}$;
⑤原式=-42×3×$\frac{1}{6}$=-21.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.


 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
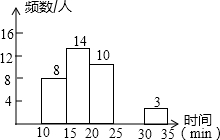 某校中午学生用餐比较拥挤,为建议学校分年级错时用餐,李老师带领数学学习小组在某天随机调查了部分学生,统计了他们从下课到就餐结束所用的时间,并绘制成统计表和如图所示的不完整统计图.
某校中午学生用餐比较拥挤,为建议学校分年级错时用餐,李老师带领数学学习小组在某天随机调查了部分学生,统计了他们从下课到就餐结束所用的时间,并绘制成统计表和如图所示的不完整统计图.| 时间分段/min | 频(人)数 | 百分比 |
| 10≤x<15 | 8 | 20% |
| 15≤x<20 | 14 | a |
| 20≤x<25 | 10 | 25% |
| 25≤x<30 | b | 12.50% |
| 30≤x<35 | 3 | 7.50% |
| 合计 | c | 100% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com