
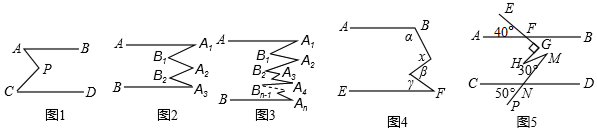
分析 (1)过点P作OP∥AB,根据两直线平行,内错角相等可得∠1=∠PAB,∠2=∠PCD,再根据∠APC=∠1+∠2整理即可得证;
(2)①过点A2作A2O∥AA1,根据(1)可得∠B1=∠A1+∠1,∠B2=∠2+∠A3,然后相加整理即可得解;②根据规律,A系列的角的和等于B系列的角的和列式即可;
(3)①过∠x的顶点作CD∥AB,然后根据平行线的性质和(1)的结论表示出x即可;②根据(2)的结论列式计算即可得解.
解答  解:(1)证明:如图1,过点P作OP∥AB,
解:(1)证明:如图1,过点P作OP∥AB,
∵AB∥CD,
∴OP∥AB∥CD,
∴∠1=∠PAB,∠2=∠PCD,
∴∠APC=∠1+∠2=∠PAB+∠PCD,
即∠APC=∠PAB+∠PCD;
(2)①如图2,过点A2作A2O∥AA1,
由(1)可知∠B1=∠A1+∠1,∠B2=∠2+∠A3,
所以,∠B1+∠B2=∠A1+∠A2+∠A3;
②如图3,由①可知:
∠A1+∠A2+…+∠An=∠B1+∠B2+…+∠Bn-1;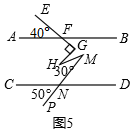
(3)①如图4,过∠x的顶点作CD∥AB,
则∠x=(180°-α)+(β-γ)=180°-α-γ+β,
②如图5,由(1)可知,40°+∠GHM+50°=∠G+∠M,
∵∠G=90°,∠M=30°,
∴∠GHM=90°+30°-40°-50°=30°.
故答案为:B;30°.
点评 本题考查了平行线的性质,熟练掌握性质并作出辅助线是解题的关键,难点在于总结出A系列的角的和等于B系列的角的和.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | (2a+b)(2a-3b) | B. | (x-2y)(x+2y) | C. | (x+1)(1+x) | D. | (-x-y)(x+y) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点E在以AB为直径的⊙O上,点C是$\widehat{BE}$的中点,过点C作CD垂直于AE,交AE的延长线于点D,连接BE交AC于点F.
如图,点E在以AB为直径的⊙O上,点C是$\widehat{BE}$的中点,过点C作CD垂直于AE,交AE的延长线于点D,连接BE交AC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 方差 | B. | 平均数 | C. | 众数 | D. | 中位数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com