
����Ŀ��ƽ��ֱ������ϵxOy�У�������Ϊa�ĵ�A�ڷ���������y1��![]() (x��0)��ͼ���ϣ���A���A���ڵ�O�Գƣ�һ�κ���y2��mx+n��ͼ����A��
(x��0)��ͼ���ϣ���A���A���ڵ�O�Գƣ�һ�κ���y2��mx+n��ͼ����A��
(1)��a��2����B(4��2)�ں���y1��y2��ͼ���ϣ�
���ֱ�����y1��y2�ı���ʽ��
��ֱ��д��ʹy1��y2��0������x�ķ�Χ��
(2)��ͼ���躯��y1��y2��ͼ���ཻ�ڵ�B����B�ĺ�����Ϊ3a����AA��B�����Ϊ16����k��ֵ��
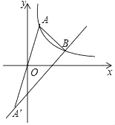
���𰸡�(1)��![]() , y2=x��2;��2<x<4��(2)6.
, y2=x��2;��2<x<4��(2)6.
��������
��1������֪��������꼴����
��2������������ת��Ϊ��AOB������ٸ���S��AOB��S�ı���ACDB���⼴�ɵý���
��1��������֪����B��4��2����y1�T![]() ��x��0����ͼ��������k��8����y1
��x��0����ͼ��������k��8����y1![]() ��
��
��a��2�����A������2��4����A����������2����4����
��B��4��2����A����2����4������y2��mx+n������![]() �������
�������![]() ����y2��x��2��
����y2��x��2��
����y1��y2��0ʱ��y1![]() ͼ����y2��x��2ͼ���Ϸ�����������ͼ����x���Ϸ�������ͼ�����2��x��4��
ͼ����y2��x��2ͼ���Ϸ�����������ͼ����x���Ϸ�������ͼ�����2��x��4��
��2���ֱ����A��B��AC��x���ڵ�C��BD��x���ڵ�D����BO��

��OΪAA���е���S��AOB![]() S��ABA����8��
S��ABA����8��
�ߵ�A��B��˫����������S��AOC��S��BOD����S��AOB��S�ı���ACDB��8��
����֪��A��B���궼��ʾΪ��a��![]() ����3a��
����3a��![]() ������
������![]() ��
��
�����k��6��


 ������������Ӧ����ϵ�д�
������������Ӧ����ϵ�д� ͬ����չ�Ķ�ϵ�д�
ͬ����չ�Ķ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڹ��ɺ��ܽ��С�����֣������ν�����dz�����ѧ�Ļ���˼�뷽�������㷺��Ӧ������ѧѧϰ�ͽ�������У���������ϵ����ͼ�����ʺ���ͼ����������������ϵ�����������µķ��֣�С�����о���ֱ��ֱ�����ҵ����ʹ����У���ͼ��ֱ��AB����CD�ڵ�E����AE=x��BE=y���ú�x��y��ʽ�ӱ�ʾͼ�е���CD�ij��ȣ���ͨ���Ƚ��˶�����CD����֮��ֱ��ֱ��AB�Ĵ�С��ϵ��������һ����������x��y�IJ���ʽ����Ҳ�ܷ����������ʽ��д���㷢�ֵIJ���ʽ��
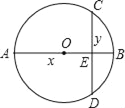
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���y=��x2+bx+c��c��0����ͼ����x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C����OB=OC=3������ΪM��
��1������κ����Ľ���ʽ��
��2����PΪ�߶�BM�ϵ�һ�����㣬����P��x��Ĵ���PQ������ΪQ����OQ=m���ı���ACPQ�����ΪS����S����m�ĺ�������ʽ����д��m��ȡֵ��Χ��
��3��̽�����߶�BM���Ƿ���ڵ�N��ʹ��NMCΪ���������Σ�������ڣ������N�����ꣻ��������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
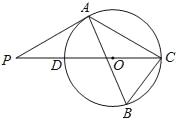
����Ŀ����ͼ����ABC�ڽ�����O����B=60�㣬CD����O��ֱ������P��CD�ӳ����ϵ�һ�㣬��AP=AC��
��1����֤��PA����O�����ߣ�
��2����AB=4+![]() ��BC=2
��BC=2![]() ������O�İ뾶��
������O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
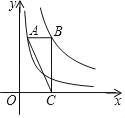
����Ŀ����ͼ����A��˫����y��![]() ��x��0���ϣ���B��˫����y��
��x��0���ϣ���B��˫����y��![]() ��x��0���ϣ���AB��x�ᣬBC��y�ᣬ��C��x���ϣ�����ABC�����Ϊ_____��
��x��0���ϣ���AB��x�ᣬBC��y�ᣬ��C��x���ϣ�����ABC�����Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺�涨![]() ������һ����λ�����ϵ���Ȼ������
������һ����λ�����ϵ���Ȼ������![]() �ĸ�λ���ַ�������������Ȼ��
�ĸ�λ���ַ�������������Ȼ��![]() ��
��![]() ��ȣ����
��ȣ����![]() Ϊ������.��
������.��![]() �����
�����![]() ����������
����������![]() ����
����![]() ���ǻ�����.���ݶ���ɵ���Ȼ������11�ǵ�1�����ֵĻ�����������Ȼ�����е�201�����ֵĻ�������__________��
���ǻ�����.���ݶ���ɵ���Ȼ������11�ǵ�1�����ֵĻ�����������Ȼ�����е�201�����ֵĻ�������__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
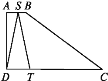
����Ŀ����ͼ�����ı���ABCD��,AB��CD����A=90����AB=1��AD=3��DC=5.��S��A��B��C�˶���C��ֹͣ����SΪԲ�ģ�SDΪ�뾶����������DC��T�㣬��S���˶���·����Ϊx��������DST�����Ϊy����y��x�ĺ���ͼ��ӦΪ( )
A. 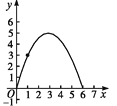 B.
B. 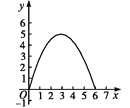
C. 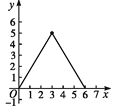 D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
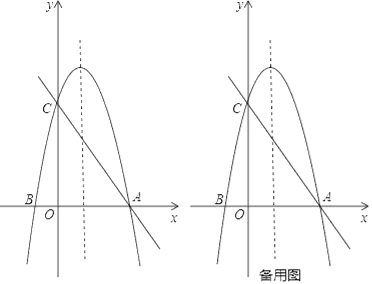
����Ŀ����ͼ����x=1Ϊ�Գ����������y=ax2+bx+c��ͼ����x�ύ�ڵ�A����B����1��0������y�ύ�ڵ�C��0��4������ֱ��AC��
��1���������߽���ʽ��
��2����P�������ߵĶԳ����ϣ��ҵ�ֱ��AC��x��ľ�����ȣ����P��������Ϊm����m��ֵ��
��3����M��y������λ�ڵ�C�Ϸ�����N��ֱ��AC�ϣ���QΪ��һ��������������һ�㣬���Ե�C��M��N��QΪ������ı��������Σ���ֱ��д����Q�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ�һ������������OC����x��ļн�Ϊ30����������OC��ȡ��A������A��AH��x���ڵ�H����������y=x2(x>0)��ȡ��P����y����ȡ��Q��ʹ����P��O��QΪ���㣬���Ե�QΪֱ�Ƕ��������������AOHȫ�ȣ�����������ĵ�A��������__________��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com