
分析 先算除法,再算加法,最后把x的值代入进行计算即可.
解答 解:原式=$\frac{(x+2)^{2}}{(x+2)(x-2)}$•$\frac{\sqrt{3}x(x-2)}{x+2}$+(7+4$\sqrt{3}$)x2
=$\sqrt{3}$x+(7+4$\sqrt{3}$)x2.
当x=2-$\sqrt{3}$时,
原式=$\sqrt{3}$(2-$\sqrt{3}$)+(7+4$\sqrt{3}$)(2-$\sqrt{3}$)2
=2$\sqrt{3}$-3+(7+4$\sqrt{3}$)(7-4$\sqrt{3}$)
=2$\sqrt{3}$-3+49-48
=2$\sqrt{3}$-2.
点评 本题考查的是分式的化简求值,分式求值题中比较多的题型主要有三种:转化已知条件后整体代入求值;转化所求问题后将条件整体代入求值;既要转化条件,也要转化问题,然后再代入求值.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
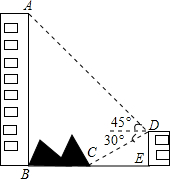 如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=80m,DE=10m,求障碍物B,C两点间的距离(结果精确到0.1m)(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=80m,DE=10m,求障碍物B,C两点间的距离(结果精确到0.1m)(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 日期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 | 4月6日 | 4月7日 |
| 气温 | 27℃ | 30℃ | 29℃ | 28℃ | 17℃ | 16℃ | 17℃ |
| A. | 10和28 | B. | 14和17 | C. | 14和27 | D. | 14和28 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
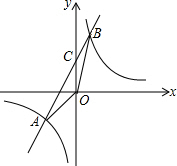 如图,已知A(n,-2),B(1,4)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点,直线AB与y轴交于点C.
如图,已知A(n,-2),B(1,4)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点,直线AB与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{3x-2y=1}\\{y=4z+1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{a=3}\\{2b-3a=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{\frac{1}{x}+y=3}\\{\frac{1}{y}+2x=4}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{mn=-1}\\{m+n=3}\end{array}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com