
【题目】取一张长方形的纸片,按如图的方法折叠,然后回答问题.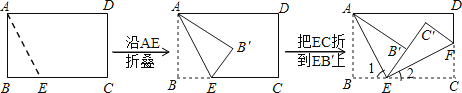
(1)分别写出∠1与∠AEC , ∠2与∠FEB之间所满足的等量关系;
(2)写出∠1与∠2之间所满足的等量关系,并说明理由;
(3)AE与EF垂直吗?为什么?
【答案】
(1)
【解答】∠1与∠AEC互补;∠2与∠FEB互补
(2)
【解答】∠1+∠2=90°.理由:
根据折叠的性质可知,∠1=∠AEB,∠2=∠FEC,
∵∠1+∠AEB+∠2+∠FEC=180°,
∴2(∠1+∠2)=180°,即∠1+∠2=90°
(3)
【解答】AE与EF垂直
∵由(2)知∵∠1+∠AEB+∠2+∠FEC=180°∠1+∠2=90°,
∴∠AEB+∠FEC=90°,
∴AE与EF垂直.
【解析】(1)由邻补角的性质直接得出.(2)根据折叠的性质可知,∠1=∠AEB , ∠2=∠FEC , 而这四个角的和为180°,从而求得∠1+∠2的度数.
【考点精析】认真审题,首先需要了解余角和补角的特征(互余、互补是指两个角的数量关系,与两个角的位置无关),还要掌握垂线的性质(垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知点E、F分别是AD、CE边上的中点,且S△BEF=4cm2 , 则S△ABC的值为( ) 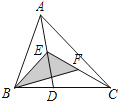
A.1cm2
B.2cm2
C.8cm2
D.16cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E.其中能使△ABC≌△AED的条件有( ) 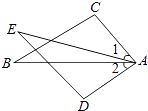
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器商场销售A、B两种型号计算器,两种计算器的进货价格分别为每台30元,40元,商场销售5台A型号和1台B型号计算器,可获利润76元;销售6台A型号和3台B型号计算器,可获利润120元.
(1)求商场销售A、B两种型号计算器的销售价格分别是多少元?(利润=销售价格﹣进货价格)
(2)商场准备用不多于2500元的资金购进A、B两种型号计算器共70台,问最少需要购进A型号的计算器多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市居民用电的电价实行阶梯收费,收费标准如下表:

(1)已知李叔家四月份用电286度,缴纳电费178.76元;五月份用电316度,缴纳电费198.56元,请你根据以上数据,求出表格中a,b的值.
(2)六月份是用电高峰期,李叔计划六月份电费支出不超过300元,那么李叔家六月份最多可用电多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校是乒乓球体育传统项目学校,为进一步推动该项目的开展,学校准备到体育用品店购买直拍球拍和横拍球拍若干副,并且每买一副球拍必须要买10个乒乓球,乒乓球的单价为2元/个,若购买20副直拍球拍和15副横拍球拍花费9000元;购买10副横拍球拍比购买5副直拍球拍多花费1600元.
(1)求两种球拍每副各多少元?
(2)若学校购买两种球拍共40副,且直拍球拍的数量不多于横拍球拍数量的3倍,请你给出一种费用最少的方案,并求出该方案所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中E是BC上的一点,EC=2EB,点D是AC的中点,AE、BD交于点F,AF=3FE.若△ABC的面积为18,给出下列命题: ①△ABE的面积为6;
②△ABF的面积和四边形DFEC的面积相等;
③点F是BD的中点;
④四边形DFEC的面积为 ![]() .
.
其中,正确的结论有 . (把你认为正确的结论的序号都填上)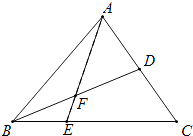
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:13=1= ![]() ×1×2213+23=9=
×1×2213+23=9= ![]() ×22×32
×22×32
13+23+33=36= ![]() ×32×42
×32×42
13+23+33+43=100= ![]() ×42×52
×42×52
…
根据上述规律计算:13+23+33+…+193+203= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com