
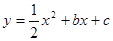 (b,c是常数,且c<0)与
(b,c是常数,且c<0)与 轴分别交于点A、B(点A位于点B的左侧),与
轴分别交于点A、B(点A位于点B的左侧),与 轴的负半轴交于点C,点A的坐标为(-1,0).
轴的负半轴交于点C,点A的坐标为(-1,0).
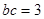 .求抛物线的解析式.
.求抛物线的解析式. 轴下方抛物线上的动点,连接PB、PC.设△PBC的面积为S.
轴下方抛物线上的动点,连接PB、PC.设△PBC的面积为S.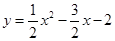 ;(3)①0<S<5;②
;(3)①0<S<5;② +c,﹣2c;11.
+c,﹣2c;11.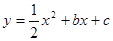 过点A (-1,0),得到:b = c+
过点A (-1,0),得到:b = c+ ,联立
,联立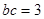 ,求出b,c的值即可;
,求出b,c的值即可;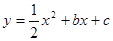 过点A (-1,0),
过点A (-1,0), ,
,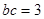 ,
,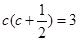 ,
,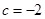 ,
,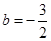 ,
,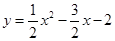 ;
;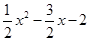 ).
). x﹣2.
x﹣2. AB•OC=5,
AB•OC=5, x﹣2),
x﹣2), x2﹣
x2﹣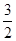 x﹣2)+(
x﹣2)+( x﹣2)=﹣
x﹣2)=﹣ x2+2x,
x2+2x, PF•OB=
PF•OB= (﹣
(﹣ x2+2x)×4=﹣x2+4x=﹣(x﹣2)2+4,
x2+2x)×4=﹣x2+4x=﹣(x﹣2)2+4,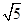 .
. BC•h,∴h=
BC•h,∴h=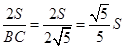 .
.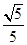 ×1=
×1=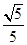 <
<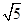 ,此时P点有1个,△PBC有1个;
,此时P点有1个,△PBC有1个;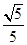 ×2=
×2=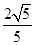 <
<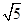 ,此时P点有1个,△PBC有1个;
,此时P点有1个,△PBC有1个;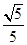 ×3=
×3=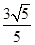 <
<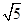 ,此时P点有1个,△PBC有1个;
,此时P点有1个,△PBC有1个;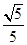 ×4=
×4=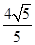 <
<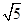 ,此时P点有1个,△PBC有1个;
,此时P点有1个,△PBC有1个; +c,﹣2c;11.
+c,﹣2c;11.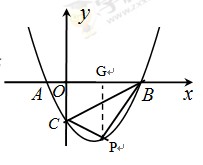 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:不详 题型:单选题
| A.b="2,c=2" | B.b=2,c=0 |
| C.b=﹣2,c=﹣1 | D.b=﹣3,c="2" |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 与坐标轴交于
与坐标轴交于 三点,点
三点,点 的横坐标为
的横坐标为 ,过点
,过点 的直线
的直线 与
与 轴交于点
轴交于点 ,点
,点 是线段
是线段 上的一个动点,
上的一个动点, 于点
于点 .若
.若 ,且
,且 .
.
 的值
的值 的坐标(其中
的坐标(其中 用含
用含 的式子表示):
的式子表示): 的变化,是否存在
的变化,是否存在 的值,使
的值,使 为等腰三角形?
为等腰三角形?查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 中,
中,  , 高
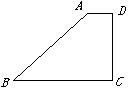
, 高 (如图1). 动点
(如图1). 动点 同时从点
同时从点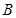 出发, 点
出发, 点 沿
沿 运动到点
运动到点 停止, 点
停止, 点 沿
沿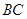 运动到点
运动到点 停止,两点运动时的速度都是1cm/s,而当点
停止,两点运动时的速度都是1cm/s,而当点 到达点
到达点 时,点
时,点 正好到达点
正好到达点 . 设
. 设 同时从点
同时从点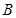 出发,经过的时间为
出发,经过的时间为 (s)时,
(s)时,  的面积为
的面积为 (如图2). 分别以
(如图2). 分别以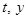 为横、纵坐标建立直角坐标系, 已知点
为横、纵坐标建立直角坐标系, 已知点 在
在 边上从
边上从 到
到 运动时,
运动时,  与
与 的函数图象是图3中的线段
的函数图象是图3中的线段 .
.

 的长度;
的长度; 在
在 边上和
边上和 边上运动时,
边上运动时,  与
与 的函数关系式(注明自变量的取值范围), 并在图3中补全整个运动中
的函数关系式(注明自变量的取值范围), 并在图3中补全整个运动中 关于
关于 的函数关系的大致图象.
的函数关系的大致图象.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 (x+1)2+3,下列结论:①抛物线的开口向下;②对称轴为直线x=1;③顶点坐标为(﹣1,3);④x>﹣1时,y随x的增大而减小,其中正确结论的个数为( )
(x+1)2+3,下列结论:①抛物线的开口向下;②对称轴为直线x=1;③顶点坐标为(﹣1,3);④x>﹣1时,y随x的增大而减小,其中正确结论的个数为( )| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 或
或 .其中正确的是( )
.其中正确的是( )
| A.①② | B.①④ | C.②③ | D.③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com