
【题目】如图,正方形OABC的边长为3,点A、C分别在x轴,y轴的正半轴上,点D(1,0)在OA上,P是OB上一动点,则PA+PD的最小值为_____.

科目:初中数学 来源: 题型:
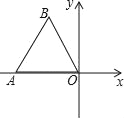
【题目】如图,边长为1的等边△ABO在平面直角坐标系的位置如图所示,点O为坐标原点,点A在x轴上,以点O为旋转中心,将△ABO按逆时针方向旋转60°,得到△OA′B′,则点A′的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD相交于点O,给出下列四组条件:①AB∥CD,AD∥BC;②AB=CD,AD=BC;③AO=CO,BO=DO;④AB∥CD,AD=BC。其中一定能判断这个四边形是平行四边形的条件共有
A. 1组 B. 2组 C. 3组 D. 4组
查看答案和解析>>
科目:初中数学 来源: 题型:
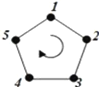
【题目】五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为3的顶点上时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的顶点;然后从1→2为第二次“移位”.若小宇从编号为4的顶点开始,第2018次“移位”后,那么他所处的顶点的编号是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
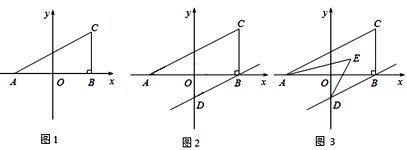
【题目】如图1,在平面直角坐标系中,A(a,0),C(b,2),且满足![]() ,过C作
,过C作![]() 轴于B,
轴于B,
(1)求a,b的值;
(2)在y轴上是否存在点P,使得△ABC和△OCP的面积相等,若存在,求出点P坐标,若不存在,试说明理由.
(3)若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,如图2,图3,
①求:∠CAB+∠ODB的度数;
②求:∠AED的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业对每个员工在当月生产某种产品的件数统计如下:设产品件数为x(单位:件),企业规定:当x<15时为不称职;当15≤x<20时为基本称职;当20≤x<25为称职;当x≥25时为优秀.解答下列问题
(1)试求出优秀员工人数所占百分比;
(2)计算所有优秀和称职的员工中月产品件数的中位数和众数;
(3)为了调动员工的工作积极性,企业决定制定月产品件数奖励标准,凡达到或超过这个标准的员工将受到奖励.如果要使得所有优秀和称职的员工中至少有一半能获奖,你认为这个奖励标准应定为多少件合适?简述其理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面文字,根据所给信息解答下面问题:把几个数用大括号括起来,中间用逗号隔开,如:{3,4};{﹣3,6,8,18},其中大括号内的数称其为集合的元素.如果一个集合满足:只要其中有一个元素a,使得﹣2a+4也是这个集合的元素,这样的集合称为条件集合.例如;{3,﹣2},因为﹣2×3+4=﹣2,﹣2恰好是这个集合的元素所以吕{3,﹣2}是条件集合:例如;(﹣2,9,8,},因为﹣2×(﹣2)+4=8,8恰好是这个集合的元素,所以{﹣2,9,8,}是条件集合.
(1)集合{﹣4,12}是否是条件集合?
(2)集合{![]() ,﹣
,﹣![]() ,
,![]() }是否是条件集合?
}是否是条件集合?
(3)若集合{8,n}和{m}都是条件集合.求m、n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列两个等式: ![]() ,
, ![]() ,给出定义如下:
,给出定义如下:
我们称使等式![]() 成立的一对有理数
成立的一对有理数![]() ,
, ![]() 为“共生有理数对”,记为(
为“共生有理数对”,记为(![]() ,
, ![]() ),如:数对(
),如:数对(![]() ,
, ![]() ),(
),(![]() ,
, ![]() ),都是“共生有理数对”.
),都是“共生有理数对”.
(1)判断数对(![]() ,
, ![]() ),(
),(![]() ,
, ![]() )是不是“共生有理数对”,写出过程;
)是不是“共生有理数对”,写出过程;
(2)若(![]() ,
, ![]() )是“共生有理数对”,求
)是“共生有理数对”,求![]() 的值;
的值;
(3)若(![]() ,
, ![]() )是“共生有理数对”,则(
)是“共生有理数对”,则(![]() ,
, ![]() ) “共生有理数对”(填“是”或“不是”);说明理由;
) “共生有理数对”(填“是”或“不是”);说明理由;
(4)请再写出一对符合条件的 “共生有理数对”为 (注意:不能与题目中已有的“共生有理数对”重复)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com