
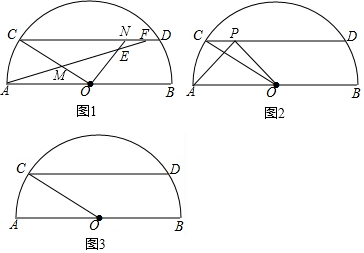
分析 (1)先判断出∠BOD=∠NDO,$\widehat{AC}=\widehat{BD}$进而得出∠AOC=∠CDO,即可得出△AMO≌△OND,结论得证;
(2)构造出直角三角形,先判断出PH=$\frac{1}{2}$OA,即可得出CG=$\frac{1}{2}$OC,进而求出∠AOC=30°,最后用角的差,即可得出结论.
(3)先求出CD=2CG=16,再判断出△AOE≌△COD,进而判断出四边形AODF是平行四边形,最后用线段的差即可得出结论;
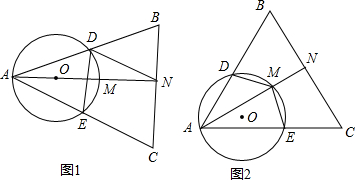
解答 解:(1)如图1,
连接OD,
∴OA=OD,
∵CD∥AB,
∴∠BOD=∠NDO,$\widehat{AC}=\widehat{BD}$,
∴∠AOC=∠BCD,
∴∠AOC=∠CDO,
在△AMO和△OND中,$\left\{\begin{array}{l}{OA=OD}\\{∠AOM=∠ODN}\\{OM=DN}\end{array}\right.$,
∴△AMO≌△OND,
∴AM=ON,
(2)如图2,
过点C作CG⊥AB,PH⊥AB,
∴CG=PH,
∵AP=OP,∠APO=90°,
∴∠AOP=45°,PH=$\frac{1}{2}$OA,
∴CG=$\frac{1}{2}$OA=$\frac{1}{2}$OC,
∴∠AOC=30°,
∴∠COP=∠AOP-∠AOC=15°.
(3)如图3,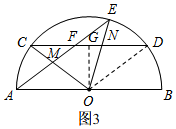
作OG⊥CD于G,连接OD,
∵AB=20,
∴OC=10
CG=OC•cos∠C=OC•cos∠AOC=10×$\frac{4}{5}$=8
∴CD=2CG=16
∵NE=NF,
∴∠E=∠EFN
∵CD∥AB,
∴∠EFN=∠A
∴∠E=∠A,
∴OE=OA
∵CD∥AB,
∴∠BOD=∠D=∠C=∠AOC
∴∠AOE=∠COD
∴△AOE≌△COD,
∴AE=CD=16
∵△AOM≌△ODN,
∴∠NOD=∠A=∠E
∴AE∥OD,
∴四边形AODF是平行四边形
∴AF=OD=10
∴EF=AE-AF=16-10=6,
点评 此题是四边形综合题,主要考查了圆的性质,平行线的性质,全等三角形的判定和性质,平行四边形的判定和性质,得出△AOE≌△COD是解本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
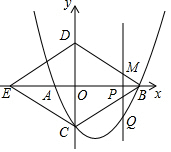 抛物线与x轴交于A,B两点,(点B在点A的左侧)且A,B两点的坐标分别为(-2,0)、(8,0),与y轴交于点C(0,-4),连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线L交抛物线于点Q,交BD于点M.
抛物线与x轴交于A,B两点,(点B在点A的左侧)且A,B两点的坐标分别为(-2,0)、(8,0),与y轴交于点C(0,-4),连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线L交抛物线于点Q,交BD于点M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
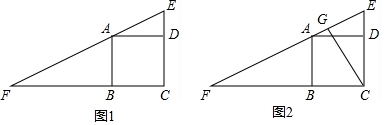
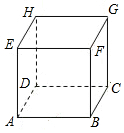 如图,一个上方无盖的正方体盒子紧贴地面,一只蚂蚁由盒外AE的中点处出发,沿着盒子面爬行到盒内的点C处,已知正方体的边长为4,问这只蚂蚁爬行的最短距离是10.
如图,一个上方无盖的正方体盒子紧贴地面,一只蚂蚁由盒外AE的中点处出发,沿着盒子面爬行到盒内的点C处,已知正方体的边长为4,问这只蚂蚁爬行的最短距离是10.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
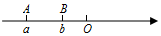 已知a、b表示两个不同点A、B的有理数,且|a|=5,|b|=2,它们在数轴的位置如图所示.
已知a、b表示两个不同点A、B的有理数,且|a|=5,|b|=2,它们在数轴的位置如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com