
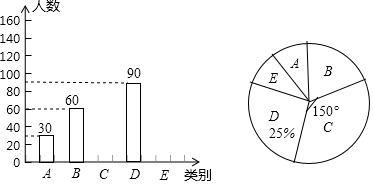
分析 (1)根据使用手机时间为D的人数和所占的百分比即可求出总人数;用总人数乘以C所占的百分比得出C类的人数,用总人数减去A、B、C、D类的人数,求出E类的人数,从而补全条形图;
(2)用全校的总人数乘以患有严重“手机瘾”的学生人数所占的百分比,即可求出答案;
(3)结合初三毕业生的手机使用情况得出答案.
解答 解:(1)根据题意得:调查的学生数为:90÷25%=360(人).
即本次共调查的学生人数为360人.
C类的人数是:360×$\frac{150}{360}$=150(人),
E类的人数是:360-(30+60+150+90)=30(人).
补全的条形图如图: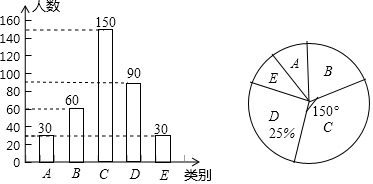
(2)该校初三毕业生中患有严重“手机瘾”的学生有:900×$\frac{90+30}{360}$=300(人);
即估计该校初三毕业生中患有严重“手机瘾”的学生有300人;
(3)该校初三毕业生中患有严重“手机瘾”的学生占$\frac{1}{3}$,应对学生使用时间提出建议,适时减少时间.
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.也考查了用样本估计总体的思想.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
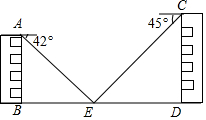 数学小组的两位同学准备测量两幢教学楼之间的距离,如图,两幢教学楼AB和CD之间有一景观池(AB⊥BD,CD⊥BD),一同学在A点测得池中喷泉处E点的俯角为42°,另一同学在C点测得E点的俯角为45°(点B,E,D在同一直线上),两个同学已经在学校资料室查出楼高AB=15m,CD=20m,求两幢教学楼之间的距离BD.
数学小组的两位同学准备测量两幢教学楼之间的距离,如图,两幢教学楼AB和CD之间有一景观池(AB⊥BD,CD⊥BD),一同学在A点测得池中喷泉处E点的俯角为42°,另一同学在C点测得E点的俯角为45°(点B,E,D在同一直线上),两个同学已经在学校资料室查出楼高AB=15m,CD=20m,求两幢教学楼之间的距离BD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 次数 | 2 | 4 | 5 | 8 |
| 人数 | 2 | 2 | 10 | 6 |
| A. | 5 | B. | 5.5 | C. | 6 | D. | 6.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
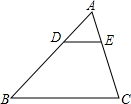 如图,在△ABC中,D、E分别为AB、AC上的点,若DE∥BC,$\frac{AD}{AB}$=$\frac{1}{3}$,则$\frac{AD+DE+AE}{AB+BC+AC}$=$\frac{1}{3}$.
如图,在△ABC中,D、E分别为AB、AC上的点,若DE∥BC,$\frac{AD}{AB}$=$\frac{1}{3}$,则$\frac{AD+DE+AE}{AB+BC+AC}$=$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
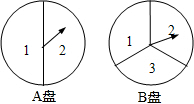 小兰和小颖用下面两个可以自由转动的转盘做游戏,每个转盘被分成面积相等的几个扇形,转动两个转盘各一次,若两次指针所指数字之和小于4,则小兰胜,否则小颖胜(指针指在分界线时重转),这个游戏对双方公平吗?请用树状图或列表法说明理由.
小兰和小颖用下面两个可以自由转动的转盘做游戏,每个转盘被分成面积相等的几个扇形,转动两个转盘各一次,若两次指针所指数字之和小于4,则小兰胜,否则小颖胜(指针指在分界线时重转),这个游戏对双方公平吗?请用树状图或列表法说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com