
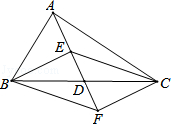
 如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,且DE=DF.给出下列条件:①BE⊥EC;②BF∥CE;③AB=AC;
如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,且DE=DF.给出下列条件:①BE⊥EC;②BF∥CE;③AB=AC;科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
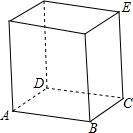 如图是一个长方体,AB=x,BC=$\frac{6}{5}$x,CE=10,则长方体的体积y与x之间的函数解析式是y=12x2,y是x的二次函数.
如图是一个长方体,AB=x,BC=$\frac{6}{5}$x,CE=10,则长方体的体积y与x之间的函数解析式是y=12x2,y是x的二次函数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图:O是矩形ABCD对角线AC、BD的交点,过点D作DE∥AC,过点C作CE∥BD,DE、CE相交于点E,连结OE交CD于点F,那么OE与DC垂直吗?请说明理由.
如图:O是矩形ABCD对角线AC、BD的交点,过点D作DE∥AC,过点C作CE∥BD,DE、CE相交于点E,连结OE交CD于点F,那么OE与DC垂直吗?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
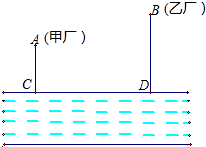 如图,在河流的一侧有甲、乙两个工厂,它们各有一条垂直于江边的小路,长度分别为4千米和5千米,若两条小路相距18千米,现要在江边建立一个抽水站,把水送到甲、乙两厂去,要使供水管长度之和最短,抽水站应建在哪里?
如图,在河流的一侧有甲、乙两个工厂,它们各有一条垂直于江边的小路,长度分别为4千米和5千米,若两条小路相距18千米,现要在江边建立一个抽水站,把水送到甲、乙两厂去,要使供水管长度之和最短,抽水站应建在哪里?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
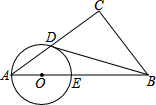 已知Rt△ABC中,∠C=90°,点O在AB上,以O为圆心OA为半径的圆与AC、AB分别交于点D、E,且∠A=∠CBD.
已知Rt△ABC中,∠C=90°,点O在AB上,以O为圆心OA为半径的圆与AC、AB分别交于点D、E,且∠A=∠CBD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中,点P(2,3),Q(3,2),请在x轴和y轴上分别找到M点和N点.使四边形PQMN周长最小.
在平面直角坐标系中,点P(2,3),Q(3,2),请在x轴和y轴上分别找到M点和N点.使四边形PQMN周长最小.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com