
分析 分三种情形①点P在AB边上,②点P在AC边上,③点P在BC边上,分别讨论计算即可.
解答 解:
如图3中,
当点P在AB边上时,∵AC=6,BC=8,∠ACB=90°,
∴AB=$\sqrt{{8}^{2}+{6}^{2}}$=10,
∵点P是△ABC的准内心,
∴∠PCB=∠PCA=45°,
∴PC=$\frac{24}{7}$;
如图4中,当点P在AC边上时,作PE⊥AB于E,设PE=x,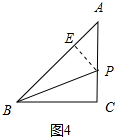
∵点P是△ABC的准内心,
∴∠PBA=∠PBC,
∵PE⊥AB,PC⊥BC,
∴PE=PC=x,BE=BC=8,
∴AE=2,
∴22+x2=(6-x)2,
解得:x=$\frac{8}{3}$;
如图5中,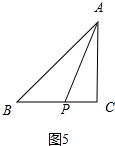
当点P在BC边上时,同理可得PC=$\frac{5}{3}$;
故答案为:$\frac{24}{7}$或$\frac{8}{3}$或$\frac{5}{3}$.
点评 本题考查角平分线的性质、勾股定理、三角形的准内心的定义等知识,解题的关键是理解题意,学会分类讨论,属于中考常考题型.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题
 如图,小华在∠AOB的内部取一点P,过点P作PE⊥OA,PF⊥OB,垂足分别为点E,F,量得PE=PF;又在边OA,OB上分别取点C,D,使OC=OD,连接PC,PD.于是,她得出结论PC=PD,你认为她的结论正确吗?请说明理由.
如图,小华在∠AOB的内部取一点P,过点P作PE⊥OA,PF⊥OB,垂足分别为点E,F,量得PE=PF;又在边OA,OB上分别取点C,D,使OC=OD,连接PC,PD.于是,她得出结论PC=PD,你认为她的结论正确吗?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com