
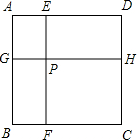
 如图边长为1的正方形ABCD被两条与边平行的线段EF、GH分割为四个小矩形,EF与GH交于点P
如图边长为1的正方形ABCD被两条与边平行的线段EF、GH分割为四个小矩形,EF与GH交于点P分析 (1)如图1中,连接AF、AH,由题意知四边形AGHD与四边形AEFB均为矩形,只要证明△ABF≌△ADH即可.
(2)结论:∠HAF=45°.设AG=a,BG=b,AE=x,ED=y.由$\left\{\begin{array}{l}{a+b=x+y}\\{2ax=by}\end{array}\right.$,推出(a+x)2=y2+b2,由y2+b2=FH2,推出a+x=FH,由AG=DH=a,AE=BF=x,推出DH+BF=FH,延长FB到M,使得BM=DH,连接AM,只要证明△ADH≌△ABM即可解决问题.
(3)如图3中,连接GF,设BG=x,BF=y,则FG=$\sqrt{{x}^{2}+{y}^{2}}$,由(x-1)(y-1)=$\frac{1}{2}$,推出xy-x-y+1=$\frac{1}{2}$,推出xy-x-y=-$\frac{1}{2}$推出x2+y2=x2+y2+1+2xy-2x-2y,推出$\sqrt{{x}^{2}+{y}^{2}}$=1-x-y,得x+y+$\sqrt{{x}^{2}+{y}^{2}}$=1,延长即可解决问题.
解答 解:(1)证明:如图1中,连接AF、AH,由题意知四边形AGHD与四边形AEFB均为矩形,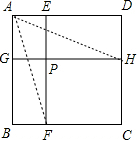
∴AG=DH,AE=BF,
∵AG=AE,
∴DH=BF,
∵四边形ABCD为正方形,
∴AB=AD,∠B=∠D=90°,
在Rt△ADH与Rt△ABF中,
$\left\{\begin{array}{l}{AB=AD}\\{∠B=∠D}\\{BF=DH}\end{array}\right.$,
∴△ABF≌△ADH,
∴AF=AH;
(2)结论:∠HAF=45°.
理由:设AG=a,BG=b,AE=x,ED=y.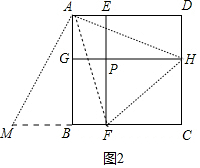
则$\left\{\begin{array}{l}{a+b=x+y}\\{2ax=by}\end{array}\right.$,
∴a-x=y-b,两边平方得a2-2ax+x2=y2-2yb+b2,
∴得a2-2ax+x2=y2-4ax+b2,
∴(a+x)2=y2+b2,
∵y2+b2=FH2,
∴a+x=FH,
∵AG=DH=a,AE=BF=x,
∴DH+BF=FH,
延长FB到M,使得BM=DH,连接AM,
∵AD=AB,∠D=∠ABM,DH=BM,
∴△ADH≌△ABM,
∴AH=AM,∠DAH=∠BAM,
∴∠MAH=∠BAD=90°,
∵AF=AF,AM=AH,FM=FH,
∴△AFM≌△AFH,
∴∠FAH=∠FAM=45°
(3)如图3中,连接GF,设BG=x,BF=y,则FG=$\sqrt{{x}^{2}+{y}^{2}}$,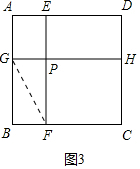
∴(x-1)(y-1)=$\frac{1}{2}$,∴xy-x-y+1=$\frac{1}{2}$,∴xy-x-y=-$\frac{1}{2}$
∴x2+y2=x2+y2+1+2xy-2x-2y,
∴$\sqrt{{x}^{2}+{y}^{2}}$=1-x-y,
得x+y+$\sqrt{{x}^{2}+{y}^{2}}$=1,
∴Rt△GBF的周长=1.
点评 此题主要考查了正方形的性质、全等三角形的判定与性质、矩形的性质,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会可以参数解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com