
 ;②∠ACB为定值60°;③∠ADB=2∠ACB;④设△ABC的面积为S,若
;②∠ACB为定值60°;③∠ADB=2∠ACB;④设△ABC的面积为S,若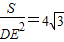 则△ABC的周长为3.
则△ABC的周长为3.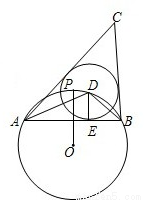
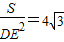 ,解出DE,继而可得出周长.
,解出DE,继而可得出周长.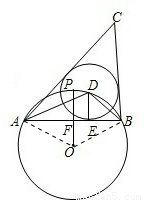
 、OA=1,在RT△AOF中,可得AF=
、OA=1,在RT△AOF中,可得AF=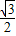 ,从而可得AB=2AF=
,从而可得AB=2AF=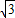 ,故①正确;
,故①正确; OA,可得∠AOF=60°,从而∠AOB=120°,即劣弧AB=120°,优弧AB=240°,从而∠ADB=120°,
OA,可得∠AOF=60°,从而∠AOB=120°,即劣弧AB=120°,优弧AB=240°,从而∠ADB=120°, (∠CAB+∠CBA)=180°,
(∠CAB+∠CBA)=180°,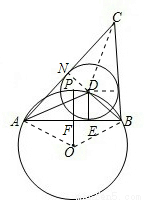
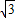 ,
, (AB+AN+CN+BC)×DE=
(AB+AN+CN+BC)×DE= (2
(2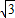 +2CN)×DE,
+2CN)×DE,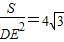 ,
,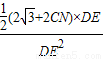 =4
=4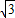 ,
,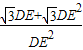 ,
, CD,
CD,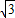 DE,
DE,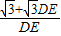 =4
=4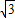 ,
, ,
,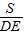 =4
=4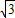 DE=
DE=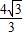 故④错误.
故④错误.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
 如图,⊙O的半径为
如图,⊙O的半径为| 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com