
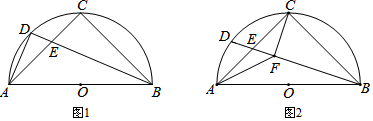
分析 (1)延长AD、BC交于点F,根据全等三角形的性质得到BE=AF,由AB是半⊙O的直径,得到BD⊥AF,根据等腰三角形的性质得到AD=DF,于是得到结论;
(2)如图2,由E为AC的中点,得到BC=AC=2CE,根据余角的性质得到∠ECF=∠CBF,根据相似三角形的性质得到$\frac{CF}{BC}$=$\frac{1}{2}$,设EF=1,则CF=2,BF=4,AE=CE=$\sqrt{5}$,BC=2$\sqrt{5}$,连接AD,得到AD=CF=2,求得根据三角形的面积得到FG=$\frac{2\sqrt{5}}{5}$,CG=$\frac{4\sqrt{5}}{5}$,于是得到结论.
解答 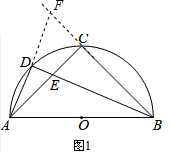 (1)证明:如图1,延长AD、BC交于点F,在△ACF与△BCE中,$\left\{\begin{array}{l}{∠CAF=∠CBE}\\{∠ACF=∠BCE=90°}\\{AC=BC}\end{array}\right.$,
(1)证明:如图1,延长AD、BC交于点F,在△ACF与△BCE中,$\left\{\begin{array}{l}{∠CAF=∠CBE}\\{∠ACF=∠BCE=90°}\\{AC=BC}\end{array}\right.$,
∴△ACF≌△BCE,
∴BE=AF,
∵AB是半⊙O的直径,
∴BD⊥AF,
∵∠ABD=∠DBC,
∴AB=BF,
∴AD=DF,
∴BE=AF=2AD;
(2)解:如图2,∵E为AC的中点,
∴BC=AC=2CE,
∵CF⊥BE,
∴∠CFE=∠CFB=∠ACB=90°,
∴∠ECF+∠CEF=∠CEF+∠CBE=90°,
∴∠ECF=∠CBF,
∴△CEF∽△CBF,
∴$\frac{EF}{CF}$=$\frac{CE}{BC}$=$\frac{1}{2}$,
∴$\frac{CF}{BC}$=$\frac{1}{2}$,
设EF=1,则CF=2,BF=4,AE=CE=$\sqrt{5}$,BC=2$\sqrt{5}$,
连接AD,
则AD⊥BD,△ADE≌△CFE,
∴AD=CF=2,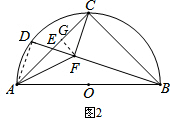
方法1:∵S△AFC=S△ABC-S△BCF-S△ABF
∴S△AFC=$\frac{1}{2}$×2$\sqrt{5}$×2$\sqrt{5}$-$\frac{1}{2}×$4×2-$\frac{1}{2}×$4×2=2,
过点F作FG⊥AC于G,
∴S△AFC=$\frac{1}{2}×$2$\sqrt{5}$×FG=2,
∴FG=$\frac{2\sqrt{5}}{5}$,CG=$\frac{4\sqrt{5}}{5}$,
∴tan∠CAF=$\frac{FG}{AG}$=$\frac{1}{3}$.
点评 本题考查了相似三角形的判定和性质,圆周角定理,全等三角形的判定和性质,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在行驶完某段全程600千米的高速公路时,李师傅对张师傅说:“你的车速太快了,平均每小时比我多跑20千米,比我少用1.5小时就跑完了全程.”
在行驶完某段全程600千米的高速公路时,李师傅对张师傅说:“你的车速太快了,平均每小时比我多跑20千米,比我少用1.5小时就跑完了全程.”查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s.设运动时间为t秒,当△PBQ为直角三角形时,t=$\frac{4}{3}$或$\frac{8}{3}$秒.
如图,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s.设运动时间为t秒,当△PBQ为直角三角形时,t=$\frac{4}{3}$或$\frac{8}{3}$秒.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
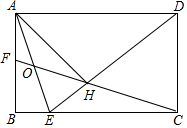 如图,在矩形ABCD中,BC=$\sqrt{2}$AB,∠ADC的平分线交边BC于点E,AH⊥DE于点H,连接CH并延长交边AB于点F,连接AE交CF于点O,给出下列命题:
如图,在矩形ABCD中,BC=$\sqrt{2}$AB,∠ADC的平分线交边BC于点E,AH⊥DE于点H,连接CH并延长交边AB于点F,连接AE交CF于点O,给出下列命题:| A. | (1)(2)(3) | B. | (2)(3)(4) | C. | (2)(4) | D. | (1)(3) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
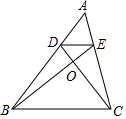 如图,在△ABC中,点D、E分别在边AB、AC上,连接CD、BE交于点O,且DE∥BC,OD=1,OC=3,AD=2,则AB的长为( )
如图,在△ABC中,点D、E分别在边AB、AC上,连接CD、BE交于点O,且DE∥BC,OD=1,OC=3,AD=2,则AB的长为( )| A. | 4 | B. | 6 | C. | 8 | D. | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com