
ЗжЮі ЃЈ1ЃЉИљОнЗжЪНЕФМгЗЈПЩвдНтД№БОЬтЃЛ
ЃЈ2ЃЉЯШЛЏМђРЈКХФкЕФЪНзгЃЌШЛКѓИљОнЗжЪНЕФГ§ЗЈПЩвдНтД№БОЬтЃЛ
ЃЈ3ЃЉИљОнЗжЪНЕФГ§ЗЈКЭМѕЗЈПЩвдЛЏМђЫљЧѓЕФЪНзгЃЌШЛКѓxЕФжЕДњШыМДПЩНтД№БОЬтЃЛ
ЃЈ4ЃЉЯШЛЏМђРЈКХФкЕФЪНзгЃЌШЛКѓИљОнЗжЪНЕФГ§ЗЈПЩвдЛЏМђЫљЧѓЕФЪНзгЃЌШЛКѓНЋmЕФжЕДњШыМДПЩНтД№БОЬтЃЎ
НтД№ НтЃКЃЈ1ЃЉ$\frac{2x}{x-2}+\frac{4}{2-x}$
=$\frac{2x-4}{x-2}$
=$\frac{2ЃЈx-2ЃЉ}{x-2}$
=2ЃЛ
ЃЈ2ЃЉЃЈ$\frac{1}{a-b}$-$\frac{b}{{a}^{2}-{b}^{2}}$ЃЉЁТ$\frac{a}{a+b}$
=$\frac{a+b-b}{ЃЈa-bЃЉЃЈa+bЃЉ}ЁС\frac{a+b}{a}$
=$\frac{a}{ЃЈa-bЃЉЃЈa+bЃЉ}ЁС\frac{a+b}{a}$
=$\frac{1}{a-b}$ЃЛ
ЃЈ3ЃЉ$\frac{x}{x+2}$ЁТ$\frac{{{x^2}-x}}{{{x^2}+4x+4}}$-$\frac{x}{x-1}$
=$\frac{x}{x+2}ЁС\frac{ЃЈx+2ЃЉ^{2}}{xЃЈx-1ЃЉ}-\frac{x}{x-1}$
=$\frac{x+2}{x-1}-\frac{x}{x-1}$
=$\frac{2}{x-1}$ЃЌ
ЕБx=1+$\sqrt{3}$ЃЌ
дЪН=$\frac{2}{1+\sqrt{3}-1}=\frac{2}{\sqrt{3}}=\frac{2\sqrt{3}}{3}$ЃЎ
ЃЈ4ЃЉ$\frac{{m}^{2}-2m+1}{{m}^{2}-1}$$ЁТЃЈm-1-\frac{m-1}{m+1}ЃЉ$
=$\frac{ЃЈm-1ЃЉ^{2}}{ЃЈm+1ЃЉЃЈm-1ЃЉ}ЁТ\frac{ЃЈm-1ЃЉЃЈm+1ЃЉ-ЃЈm-1ЃЉ}{m+1}$
=$\frac{m-1}{m+1}ЁТ\frac{mЃЈm-1ЃЉ}{m+1}$
=$\frac{m-1}{m+1}ЁС\frac{m+1}{mЃЈm-1ЃЉ}$
=$\frac{1}{m}$ЃЌ
ЕБm=$\sqrt{3}$ЪБЃЌдЪН=$\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$ЃЎ
ЕуЦР БОЬтПМВщЖўДЮИљЪНЕФЛЏМђЧѓжЕЁЂЗжЪНЕФЛЏМђЧѓжЕЃЌНтЬтЕФЙиМќЪЧУїШЗЫќУЧЕФМЦЫуЗНЗЈЃЎ


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
 ШчЭМЃЌЁїABCЕФЭтаФЮЊOЃЌШєЁЯABC=40ЁуЃЌЁЯACB=72ЁуЃЌЧѓЁЯBOCЃЎ
ШчЭМЃЌЁїABCЕФЭтаФЮЊOЃЌШєЁЯABC=40ЁуЃЌЁЯACB=72ЁуЃЌЧѓЁЯBOCЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
 ЬНОПЃКШчЭМЃЌвбжЊжБЯпl1ЁЮl2ЃЌжБЯпl3КЭжБЯпl1ЁЂl2НЛгкЕуCКЭЕуDЃЌжБЯпl3гавЛЕуP
ЬНОПЃКШчЭМЃЌвбжЊжБЯпl1ЁЮl2ЃЌжБЯпl3КЭжБЯпl1ЁЂl2НЛгкЕуCКЭЕуDЃЌжБЯпl3гавЛЕуPВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
 ШчЭМЃЌCDЗжБ№НЛADЃЌEGгкЕуDЃЌGЃЌEBЗжБ№НЛADЃЌEGгкЕуAЃЌEЃЌACНЛEGгкЕуFЃЌFHНЛADгкЕуHЃЌADЦНЗжЁЯBACЃЌEGЁЮADЃЌCGЁЭEGЃЌЁЯC=ЁЯAFHЃЎ
ШчЭМЃЌCDЗжБ№НЛADЃЌEGгкЕуDЃЌGЃЌEBЗжБ№НЛADЃЌEGгкЕуAЃЌEЃЌACНЛEGгкЕуFЃЌFHНЛADгкЕуHЃЌADЦНЗжЁЯBACЃЌEGЁЮADЃЌCGЁЭEGЃЌЁЯC=ЁЯAFHЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
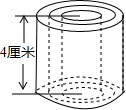 ШчЭМЫљЪОЃЌдВжљЕФИпЪЧ4РхУзЃЌЕБдВжљЕзУцАыОЖrЃЈcmЃЉБфЛЏЪБЃЌдВжљЕФЬхЛ§VЃЈcm3ЃЉвВЫцжЎБфЛЏЃЎ
ШчЭМЫљЪОЃЌдВжљЕФИпЪЧ4РхУзЃЌЕБдВжљЕзУцАыОЖrЃЈcmЃЉБфЛЏЪБЃЌдВжљЕФЬхЛ§VЃЈcm3ЃЉвВЫцжЎБфЛЏЃЎВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com