
分析 (1)首先假设这个球队胜x场,则负了(8-3-x)场,利用得分情况得出答案即可;
(2)利用现已比赛了8场,平了3场,得15分,即可得出打满15场比赛最高能得15+(15-8)×3=36(分).
(3)由题意知,以后的7场比赛中,只要分不低于(28-15=13分)即可,进而得出答案.
解答 解:(1)设这个球队胜x场,则负了(8-3-x)场.
根据题意,得3x+3×1=15.
解得x=4.
故前8场比赛中,七(1)班足球队共胜了4场.
(2)打满15场比赛最高能得
15+(15-8)×3
=15+21
=36(分).
故最高得分得36分.
(3)由题意知,以后的7场比赛中,只要分不低于(28-15=13分)即可.
所以胜不少于5场,一定达到预期目标,而胜3场、平4场,正好达到预期目标.
所以在以后的比赛中这个球队至少要胜3场.
点评 此题主要考查了一元一次方程的应用,根据已知胜负得分情况正确得出等式方程是解题关键.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
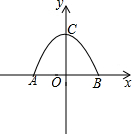 某小区的大门是如图所示的一个抛物线形状的门窗,门洞的高为4m,门洞地面的宽为6米,建立如图所示的平面直角坐标系,使抛物线的对称轴为y轴.
某小区的大门是如图所示的一个抛物线形状的门窗,门洞的高为4m,门洞地面的宽为6米,建立如图所示的平面直角坐标系,使抛物线的对称轴为y轴.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com