
 如图,△ABC为等腰直角三角形,AB=AC,∠BAC=90°,点D在线段AB上,连接CD,∠ADC=60°,AD=2,过C作CE⊥CD,且CE=CD,连接DE,交BC于F.
如图,△ABC为等腰直角三角形,AB=AC,∠BAC=90°,点D在线段AB上,连接CD,∠ADC=60°,AD=2,过C作CE⊥CD,且CE=CD,连接DE,交BC于F.分析 (1)在Rt△ACD中,求出CD即可解决问题;
(2)在EF上取一点M,使得EM=DF,只要证明△MCF是等边三角形即可解决问题.
解答 (1)解:在Rt△ADC中,∵AD=2,∠ADC=60°,
∴∠ACD=30°,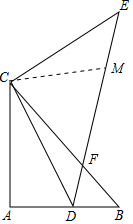
∴CD=CE=2AD=4,
∵EC⊥CD,
∴∠ECD=90°,
∴S△ECD=$\frac{1}{2}$•CD•CE=$\frac{1}{2}$×4×4=8.
(2)证明:在EF上取一点M,使得EM=DF,
∵EC=CD,∠E=∠CDF=45°,
∴△ECM≌△DCF,
∴CM=CF,
∵∠ADC=60°,
∠FDB=180°-60°-45°=75°,
∴∠DFB=∠CFM=180°-75°-45°=60°,
∴△CFM是等边三角形,
∴CF=MF,
∴EF=EM+MF=DF+CF.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的性质、勾股定理、直角三角形30度角性质、等边三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.


 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
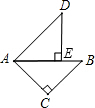 如图,△ABC与△ADE都是等腰直角三角形,∠C和∠AED都是直角,点E在AB上,如果,△ABC旋转后能与△ADE重合,那么哪一点是旋转中心?旋转了多少度?
如图,△ABC与△ADE都是等腰直角三角形,∠C和∠AED都是直角,点E在AB上,如果,△ABC旋转后能与△ADE重合,那么哪一点是旋转中心?旋转了多少度?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,已知菱形ABCD顶点的坐标分别为A(1,-1),B(5,a),C(1,3),D(b,c),在图中画出菱形ABCD,并写出a,b,c的值.
如图,在平面直角坐标系中,已知菱形ABCD顶点的坐标分别为A(1,-1),B(5,a),C(1,3),D(b,c),在图中画出菱形ABCD,并写出a,b,c的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
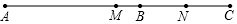 如图,点B在线段AC上,点M、N分别是AC、BC的中点.
如图,点B在线段AC上,点M、N分别是AC、BC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com