
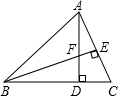
 如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为点D,E,AD与BE相交于点F,若BF=AC,求证:BD=AD.
如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为点D,E,AD与BE相交于点F,若BF=AC,求证:BD=AD.  天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
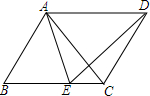 如图,在四边形ABCD中,AD∥BC,AD=BC,E为BC边上一点,且AB=AE.(1)求证:△ABC≌△EAD;
如图,在四边形ABCD中,AD∥BC,AD=BC,E为BC边上一点,且AB=AE.(1)求证:△ABC≌△EAD;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
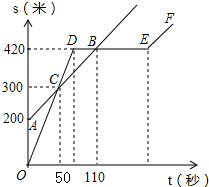 巴蜀中学的小明和朱老师一起到一条笔直的跑道上锻炼身体,到达起点后小明做了一会准备活动朱老师先跑.当小明出发时,朱老师已经距起点200米了.他们距起点的距离s(米)与小明出发的时间t(秒)之间的关系如图所示(不完整).根据图中给出的信息,解答下列问题:
巴蜀中学的小明和朱老师一起到一条笔直的跑道上锻炼身体,到达起点后小明做了一会准备活动朱老师先跑.当小明出发时,朱老师已经距起点200米了.他们距起点的距离s(米)与小明出发的时间t(秒)之间的关系如图所示(不完整).根据图中给出的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
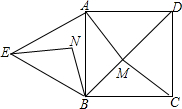 如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.
如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com