
【题目】如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A6B6A7的边长为( ) 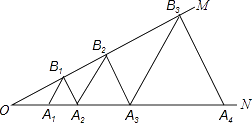
A.6
B.12
C.32
D.64
【答案】C
【解析】解:∵△A1B1A2是等边三角形, ∴A1B1=A2B1 , ∠3=∠4=∠12=60°,
∴∠2=120°,
∵∠MON=30°,
∴∠1=180°﹣120°﹣30°=30°,
又∵∠3=60°,
∴∠5=180°﹣60°﹣30°=90°,
∵∠MON=∠1=30°,
∴OA1=A1B1=1,
∴A2B1=1,
∵△A2B2A3、△A3B3A4是等边三角形,
∴∠11=∠10=60°,∠13=60°,
∵∠4=∠12=60°,
∴A1B1∥A2B2∥A3B3 , B1A2∥B2A3 ,
∴∠1=∠6=∠7=30°,∠5=∠8=90°,
∴A2B2=2B1A2 , B3A3=2B2A3 ,
∴A3B3=4B1A2=4,
A4B4=8B1A2=8,
A5B5=16B1A2=16,
以此类推:A6B6=32B1A2=32.
故选:C.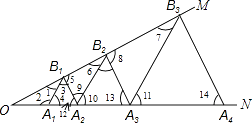
【考点精析】利用等边三角形的性质和含30度角的直角三角形对题目进行判断即可得到答案,需要熟知等边三角形的三个角都相等并且每个角都是60°;在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.


科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD,AB=6,点E在边CD上,CE=2DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FCA=3.6,其中正确结论是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的内角∠ABC与外角∠ACD的平分线交于点E,且CE∥AB,AC与BE交于点E,则下列结论错误的是( )
A.CB=CE
B.∠A=∠ECD
C.∠A=2∠E
D.AB=BF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程或方程组解应用题:
近年来,我国逐步完善养老金保险制度.甲、乙两人计划用相同的年数分别缴纳养老保险金15万元和10万元,甲计划比乙每年多缴纳养老保险金0.2万元.求甲、乙两人计划每年分别缴纳养老保险金多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为1的小正方形网格中,△AOB的顶点均在格点上.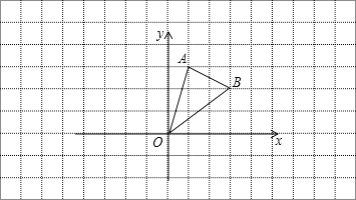
(1)B点关于y轴的对称点坐标为;
(2)将△AOB向左平移3个单位长度,再向上平移2个单位长度得到△A1O1B1 , 请画出△A1O1B1;
(3)在(2)的条件下,△AOB边AB上有一点P的坐标为(a,b),则平移后对应点P1的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家与学校在同一直线上且相距720m,一天早上他和弟弟都匀速步行去上学,弟弟走得慢,先走1分钟后,小明才出发,已知小明的速度是80m/分,以小明出发开始计时,设时间为x(分),兄弟两人之间的距离为ym,图中的折线是y与x的函数关系的部分图象,根据图象解决下列问题: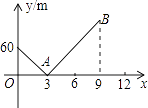
(1)弟弟步行的速度是m/分,点B的坐标是;
(2)线段AB所表示的y与x的函数关系式是;
(3)试在图中补全点B以后的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
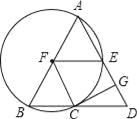
【题目】如图,在△ABD中,AB=AD,以AB为直径的⊙F交BD于点C,交AD与点E,CG⊥AD于点G.
(1)求证:GC是⊙F的切线;
(2)填空:①若△BCF的面积为15,则△BDA的面积为 .
②当∠GCD的度数为 时,四边形EFCD是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com