
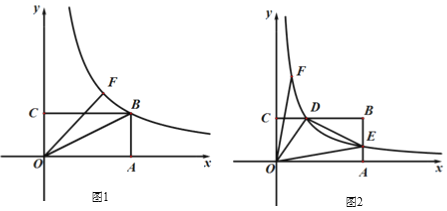
【题目】如图,四边形OABC为矩形,点B坐标为(4,2),A,C分别在x轴,y轴上,点F在第一象限内,OF的长度不变,且反比例函数![]() 经过点F.
经过点F.
(1)如图1,当F在直线y = x上时,函数图象过点B,求线段OF的长.
(2)如图2,若OF从(1)中位置绕点O逆时针旋转,反比例函数图象与BC,AB相交,交点分别为D,E,连结OD,DE,OE.
①求证:CD=2AE.
②若AE+CD=DE,求k.
③设点F的坐标为(a,b),当△ODE为等腰三角形时,求(a+b)2的值.
【答案】(1)OF =4;(2)①证明见解析;② k=![]() ;③96-16
;③96-16![]() 或36-4
或36-4![]() .
.
【解析】分析(1)由y=![]() 经过点B (2,4).,求出k的值,再利用F在直线y = x,求出m的值,最后利用勾股定理求解即可;(2) ①利用反比例函数k的几何意义可求解; ②Rt△EBD中,分别用n表示出BD、BE、DE,再利用勾股定理解答即可; ③分三种情况讨论即可:OE=OD;
经过点B (2,4).,求出k的值,再利用F在直线y = x,求出m的值,最后利用勾股定理求解即可;(2) ①利用反比例函数k的几何意义可求解; ②Rt△EBD中,分别用n表示出BD、BE、DE,再利用勾股定理解答即可; ③分三种情况讨论即可:OE=OD;
OE=DE;OD=DE.
(1)∵F在直线y=x上
∴设F(m,m)
作FM⊥x轴
∴FM=OM=m
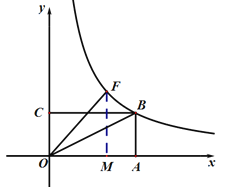
∵y=![]() 经过点B (2,4).
经过点B (2,4).
∴k=8
∴![]()
∴![]()
∴![]()
∴OF =4;
(2)①∵函数![]() 的图象经过点D,E
的图象经过点D,E
∴![]() ∵ OC=2,OA=4
∵ OC=2,OA=4
∴CO=2AE
②由①得:CD=2AE
∴可设:CD=2n,AE=n
∴DE=CD+AE=3n
BD=4-2n, BE=2-n
在Rt△EBD,由勾股定理得:![]()
∴![]()
解得![]()
![]()
③CD=2c,AE=c
情况一:若OD=DE
∴![]()
∴![]()
∴![]()
![]()
情况二:若OE=DE
![]()
∴![]()
∴![]()
情况三:OE=OD 不存在.


科目:初中数学 来源: 题型:
【题目】某学校初一年级参加社会实践课,报名第一门课的有x人,第二门课的人数比第一门课的![]() 少20人,现在需要从报名第二门课的人中调出10人学习第一门课,那么:
少20人,现在需要从报名第二门课的人中调出10人学习第一门课,那么:
(1)报两门课的共有多少人?
(2)调动后,报名第一门课的人数为 人,第二门课人数为 人.
(3)调动后,报名第一门课比报名第二门课多多少人?计算出代数式后,请选择一个你觉得合适的x的值代入,并求出具体的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请根据图中提供的信息,回答下列问题

(1)一个暖瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的暖瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定: 这两种商品都打九折;乙商场规定:买一个暖瓶赠送一个水杯。若某单位想要买4个暖瓶和15个水杯,请问选择哪家商场购买更合算,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】夏季空调销售供不应求,某空调厂接到一份紧急订单,要求在10天内(含10天)完成任务,为提高生产效率,工厂加班加点,接到任务的第一天就生产了空调42台,以后每天生产的空调都比前一天多2台,由于机器损耗等原因,当日生产的空调数量达到50台后,每多生产一台,当天生产的所有空调,平均每台成本就增加20元.
(1)设第x天生产空调y台,直接写出y与x之间的函数解析式,并写出自变量x的取值范围.
(2)若每台空调的成本价(日生产量不超过50台时)为2000元,订购价格为每台2920元,设第x天的利润为W元,试求W与x之间的函数解析式,并求工厂哪一天获得的利润最大,最大利润是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
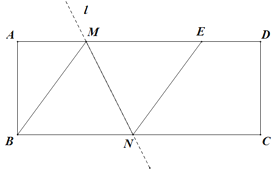
【题目】如图,在矩形ABCD中,AB=4,AD=10,点E在AD边上,已知B、E两点关于直线l对称,直线l分别交AD、BC边于点M、N,连接BM、NE.
(1)求证:四边形BMEN是菱形;
(2)若DE=2,求NC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,对角线AC与BD相交于O,AB=6cm, ∠BAO=30°,点F为AB的中点.
(1)求OF的长度;
(2)求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
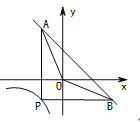
【题目】如图,P为反比例函数![]() (x<0)在第三象限内图象上的一点,过点P分别作x轴、y轴的垂线交一次函数y=-x+4的图像于点A、B.若AO、BO分别平分∠BAP,∠ABP ,则k的值为___________.
(x<0)在第三象限内图象上的一点,过点P分别作x轴、y轴的垂线交一次函数y=-x+4的图像于点A、B.若AO、BO分别平分∠BAP,∠ABP ,则k的值为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
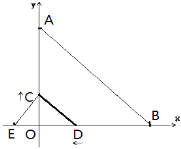
【题目】如图,已知点A(0,8)、B(8,0)、E(-2,0),动点 C从原点O出发沿OA方向以每秒1个单位长度向点A运动,动点D从点B出发沿BO方向以每秒2个单位长度向点O运动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动,设运动时间为t 秒。
(1)填空:直线AB的解析式是_____________________;
(2)求t的值,使得直线CD∥AB;
(3)是否存在时刻t,使得△ECD是等腰三角形?若存在,请求出一个这样的t值;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com