10、梯形ABCD的面积被对角线BD分成3：7两部分，它的面积被中位线分成的两部分的比是

2：3

．

分析：由梯形ABCD的面积被对角线BD分成3：7两部分，可得上底和下底的比为3：7，设上底和下底分别为3k，7k，中位线分两个梯形的高为h，然后计算面积，求比值即可．

解答：解：∵梯形ABCD的面积被对角线BD分成3：7两部分，两三角形的高相等，
∴上底和下底的比为3：7，
可设上底和下底分别为3k，7k，则中位线长：（3k+7k）÷2=5k，
∵中位线分两个梯形的高相等，为h，
∴被中位线分成的两部分的面积分别为：（3k+5k）÷2=4k，（5k+7k）÷2=6k，
∴被中位线分成的两部分的比是4k：6k=2：3．
故答案为：2：3．

点评：此题主要考查梯形中位线的性质，注意中位线分两个梯形的高相等，难度中等．

练习册系列答案

寒假作业江西人民出版社系列答案

寒假作业重庆出版社系列答案

智乐文化寒假作业期末综合复习东南大学出版社系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

如图①所示，在直角梯形ABCD中，∠BAD=90°，E是直线AB上一点，过E作直线l∥BC，交直线CD于点F．将直线l向右平移，设平移距离BE为t（t≥0），直角梯形ABCD被直线l扫过的面积（图中阴影部分）为S，S关于t的函数图象如图②所示，OM为线段，MN为抛物线的一部分，NQ为射线，N点横坐标为4．

信息读取
（1）梯形上底的长AB=

；
（2）直角梯形ABCD的面积=

；
图象理解
（3）写出图②中射线NQ表示的实际意义；
（4）当2＜t＜4时，求S关于t的函数关系式；
问题解决
（5）当t为何值时，直线l将直角梯形ABCD分成的两部分面积之比为1：3．

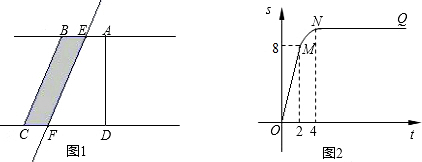
查看答案和解析>>

科目：初中数学 来源：2011-2012学年江苏省淮安市中考模拟数学试卷（解析版） 题型：解答题

如图①所示，在直角梯形ABCD中，∠BAD=90°，E是直线AB上一点，过E作直线//BC，交直线CD于点F．将直线向右平移，设平移距离BE为 (t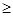0)，直角梯形ABCD被直线扫过的面积（图中阴影部份）为S，S关于的函数图象如图②所示，OM为线段，MN为抛物线的一部分，NQ为射线，N点横坐标为4．