
【题目】如图,正方形![]() 中,
中,![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,
上,![]() ,
,![]() 相交于点
相交于点![]() ,若
,若![]() ,
,![]() ,则
,则![]() __________.
__________.

科目:初中数学 来源: 题型:
【题目】在“母亲节”期间,某校部分团员参加社会公益活动,准备购进一批许愿瓶进行
销售,并将所得利润捐给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y(个)于销售单价x(元
/个)之间的对应关系如图所示.
(1)试判断y与x之间的函数关系,并求出函数关系式;
(2)若许愿瓶的进价为6元/个,按照上述市场调查销售规律,求利润w(元)与销售单价x(元/个)之间的
函数关系式;
(3)若许愿瓶的进货成本不超过900元,要想获得最大利润,试求此时这种许愿瓶的销售单价,并求出
最大利润.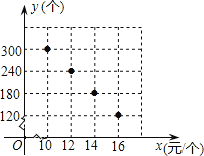
查看答案和解析>>
科目:初中数学 来源: 题型:
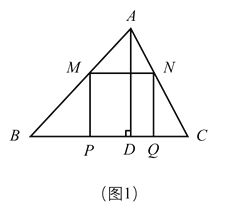
【题目】如图在锐角![]() 中,
中,![]() ,高
,高![]() ,两动点
,两动点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上滑动(不包含端点),且
上滑动(不包含端点),且![]() ,以
,以![]() 为边长向下作正方形
为边长向下作正方形![]() ,设
,设![]() ,正方形
,正方形![]() 与
与![]() 公共部分的面积为
公共部分的面积为![]() .
.
(1)如图(1),当正方形![]() 的边
的边![]() 恰好落在
恰好落在![]() 边上时,求
边上时,求![]() 的值.
的值.
(2)如图(2),当![]() 落
落![]() 外部时,求出
外部时,求出![]() 与
与![]() 的函数关系式(写出
的函数关系式(写出![]() 的取值范围)并求出
的取值范围)并求出![]() 为何值时
为何值时![]() 最大,最大是多少?
最大,最大是多少?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 交x轴于A.B两点,交y轴于点C,抛物线的对称轴交x轴于点E,点B的坐标为(1,0).
交x轴于A.B两点,交y轴于点C,抛物线的对称轴交x轴于点E,点B的坐标为(1,0).
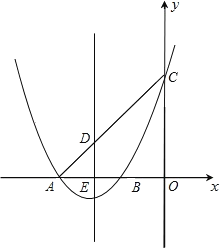
(1)求抛物线的对称轴及点A的坐标;
(2)连结CA与抛物线的对称轴交于点D.
①在对称轴上找一点P,使ΔAPC为直角三角形,求点P的坐标.
②在抛物线上是否存在点M,使得直线CM把四边形DEOC分成面积相等的两部分?若存在,请求出直线CM的解析式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有四个分别标有1、2、3、4的小球,它们的形状、大小等完全相同.小明先从口袋里随机不放回地取出一个小球,记下数字为x;小红在剩下有三个小球中随机取出一个小球,记下数字y.
(1)计算由x、y确定的点(x,y)在函数y=﹣x+6图象上的概率;
(2)小明、小红约定做一个游戏,其规则是:若x、y满足xy>6,则小明胜;若x、y满足xy<6,则小红胜.这个游戏规则公平吗?说明理由;若不公平,怎样修改游戏规则才对双方公平?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c的图象与x轴交于A(4,0),B两点,与y轴交于点C(0,2),对称轴x=1,与x轴交于点H.
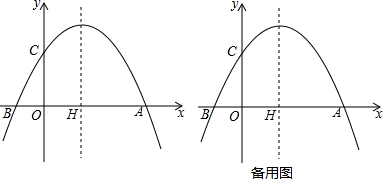
(1)求抛物线的函数表达式;
(2)直线y=kx+1(k≠0)与y轴交于点E,与抛物线交于点 P,Q(点P在y轴左侧,点Q在y轴右侧),连接CP,CQ,若△CPQ的面积为![]() ,求点P,Q的坐标;
,求点P,Q的坐标;
(3)在(2)的条件下,连接AC交PQ于G,在对称轴上是否存在一点K,连接GK,将线段GK绕点G顺时针旋转90°,使点K恰好落在抛物线上,若存在,请直接写出点K的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图(1)所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图(2)所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的是( )
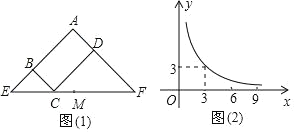
A.当x=3时,EC<EM
B.当y=9时,EC>EM
C.当x增大时,ECCF的值增大
D.当x变化时,四边形BCDA的面积不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 某学校为了了解九年级学生的体能情况,抽取了部分学生进行了体能测试,学生的测试成绩分四类:A:优秀;B:良好;C:合格;D不合格,将抽测学生的成绩绘制成如下两幅不完整的统计图,请根据统计图解答下列问题:
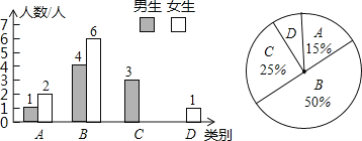
(1)求本次调查的学生总人数;
(2)成绩为C的女生有______人,成绩为D的男生有______人;
(3)扇形统计图中成绩为D的学生所对应的扇形的圆心角度数为______;
(4)补全条形统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
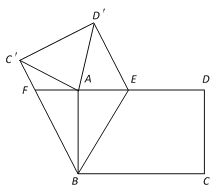
【题目】如图,在矩形ABCD中,AB=4,AD=6,E是AD边上的一个动点,将四边形BCDE沿直线BE折叠,得到四边形BC′D′E,连接AC′,AD′.
(1)若直线DA交BC′于点F,求证:EF=BF;
(2)当AE=![]() 时,求证:△AC′D′是等腰三角形;
时,求证:△AC′D′是等腰三角形;
(3)在点E的运动过程中,求△AC′D′面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com