
�� �֣���ͼ��������
�֣���ͼ�������� �Ķ���Ϊ
�Ķ���Ϊ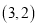 ��
��
��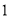 ����������
����������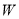 �ĺ�������ʽ��
�ĺ�������ʽ��
�� ������������
������������ ��
�� ����
���� ��Գƣ���������
��Գƣ���������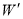 �ĺ�������ʽ��
�ĺ�������ʽ��
�� ���ڣ�
���ڣ� ���Ļ����ϣ���
���Ļ����ϣ���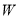 �ϵĵ�
�ϵĵ� ��
�� ʼ����
ʼ���� �ϵĵ�
�ϵĵ� ��
��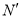 �ֱ����
�ֱ���� ��Գƣ��Ƿ���ڵ�
��Գƣ��Ƿ���ڵ� ��
�� ��
�� ��
�� �ֱ�λ�������߶Գ������࣬��
�ֱ�λ�������߶Գ������࣬�� ��
�� ����ࣩ��ʹ�ı���
����ࣩ��ʹ�ı���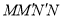 Ϊ�����Σ�
������
�����ڣ������ �����ꣻ�������ڣ�˵�����ɣ�
�����ꣻ�������ڣ�˵�����ɣ�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017-2018ѧ�����꼶��ѧ�˽̰��ϲ��4�� ����ͼ�γ��� ��Ԫ���Ծ� ���ͣ������
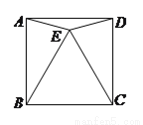
��ͼ��������ֱ�����dzߵĶ��������һ��
(1)����DCE��35�㣬���ACB�Ķ�����
(2)����ACB��140�㣬���DCE�Ķ�����
(3)�����ACB���DCE�Ĺ�ϵ����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ��ɽ��ʡ��������У���꼶���ϣ���һ��������ѧ�Ծ� ���ͣ���ѡ��
��֪��|m��2|+��n��1��2=0����2m+x=n�Ľ�Ϊ��������
A. x=��4 B. x=��3 C. x=��2 D. x=��1
B ����������|m��2|+��n��1��2=0�� �࣬ �࣬ ��̿ɻ�Ϊ�� �����. ��ѡB.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ����ѧ����ĩ��ѧ���������꼶��ѧ�Ծ� ���ͣ���ѡ��
���������У�����ȷ���ǣ�������
A. �Խ�����ȵ�ƽ���ı����Ǿ���
B. ��һ����Ϊ60��ĵ����������ǵȱ�������
C. ֱ��������б���ϵĸߵ���б�ߵ�һ��
D. �����ε������Խ�������һ��ഹֱƽ��
C ��������������������ݾ��Ρ��ȱ������Ρ�ֱ�������μ������ε����ʽ�����һ�жϣ� �������� A����ȷ���Խ�����ȵ�ƽ���ı����Ǿ��Σ����ھ��ε��ж��� B����ȷ����һ����Ϊ60��ĵ����������ǵȱ����������ڵȱ������ε��ж��� C������ֱ��������б���ϵ����ߵ���б�ߵ�һ�룻 D����ȷ���������ε����ʣ� ��ѡC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ����ѧ����ĩ��ѧ���������꼶��ѧ�Ծ� ���ͣ������
���Ҷ�ҩƷʵʩ�۸������ijҩƷ�������ν��ۺ�ÿ�еļ۸���ԭ����60Ԫ����48.6Ԫ����ôƽ��ÿ�ν��۵İٷ�����________________��
10% �������������������ƽ��ÿ�ν��۵İٷ���Ϊx��ij��ҩƷ�������ν��ۺ�ÿ�еļ۸���ԭ����60Ԫ����48.6Ԫ�����з��̣�60��1-x��2=48.6�� �ʴ�Ϊ��60��1-x��2=48.6���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2018����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
�� �֣���ͼ����
�֣���ͼ���� ��
�� ��
�� ��
��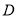 ��ͬһֱ���ϣ���
��ͬһֱ���ϣ��� ��
�� �ֱ���ֱ��
�ֱ���ֱ�� �����࣬��
�����࣬�� ��
��  ��
��  ��
��
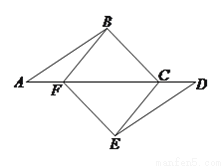
��1����֤���ı��� ��ƽ���ı��Σ�
��ƽ���ı��Σ�
��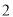 ��Ҫʹ�ı���
��Ҫʹ�ı���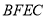 Ϊ���Σ���Ҫ����һ��������������������������е�__________��������֤����
Ϊ���Σ���Ҫ����һ��������������������������е�__________��������֤����
��
��
������ ��
�� 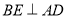
������ ��
�� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2018����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
�������� �ڣ���
�ڣ���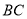 Ϊ�����ȱ�
Ϊ�����ȱ� ������
������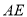 ��
�� ����
����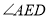 �Ĵ�СΪ__________��
�Ĵ�СΪ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�꼶��ѧ�²�ڶ�ʮ���� ������ ���ͣ������
��ͼ��һ��ֱ����ˮƽ�����ϵ�ľ��AB�ڵƹ����γ�Ӱ�ӣ���ľ���Ƶ�A����ʱ�뷽����תֱ���������ʱ��Ӱ�ӵij��ȷ����仯����AB��ֱ�ڵ���ʱ��Ӱ��ΪAC���ٶ�AC��AB����Ӱ�������ֵΪm����СֵΪn����ô���н��ۣ���m��AC����m��AC����n��AB����Ӱ�ӵij�����������С�����У���ȷ���۵������________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰����꼶�²���ѧ�������ཻ����ƽ���ߵ�Ԫ���� ���ͣ������
��֪����ͼ��AE��BC��FG��BC����1=��2����D=��3+60�㣬��CBD=70�㣮
��1����֤��AB��CD��
��2�����C�Ķ�����

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com