
����Ŀ����ƽ��ֱ������ϵ![]() �еĵ�P��ͼ��M���������µĶ��壺����ͼ��M����һ��Q��ʹ��P��Q�����ľ���С�ڻ����1�����PΪͼ��M�Ĺ�������
�еĵ�P��ͼ��M���������µĶ��壺����ͼ��M����һ��Q��ʹ��P��Q�����ľ���С�ڻ����1�����PΪͼ��M�Ĺ�������
��1������O�İ뾶Ϊ2ʱ��
���ڵ�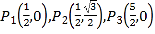 �У���O�Ĺ�������_______________��
�У���O�Ĺ�������_______________��
�ڵ�P��ֱ��y=-x�ϣ���PΪ��O �Ĺ����㣬���P�ĺ������ȡֵ��Χ��
��2����C ��Բ����x���ϣ��뾶Ϊ2��ֱ��y=-x+1��x�ᡢy�ύ�ڵ�A��B�����߶�AB�ϵ����е㶼����C�Ĺ����㣬ֱ��д��Բ��C�ĺ������ȡֵ��Χ��
���𰸡���1����P2��P3���ڣ�![]() ��x�ܣ�
��x�ܣ�![]() ��
��![]() ��x��
��x��![]() ����2����2��x��1��2��x��2
����2����2��x��1��2��x��2![]() .
.
��������
���⣨1����������ã�Pֻ������OΪԲ�ģ��뾶Ϊ1��3��Բ֮�伴�ɣ���![]() ��ֵ��֪
��ֵ��֪![]() Ϊ��O�Ĺ����㣻������������Pֻ������OΪԲ�ģ��뾶Ϊ1��3��Բ֮�伴�ɣ�����P�����귶Χ����
Ϊ��O�Ĺ����㣻������������Pֻ������OΪԲ�ģ��뾶Ϊ1��3��Բ֮�伴�ɣ�����P�����귶Χ����![]() ��x�ܣ�
��x�ܣ�![]() ��
��![]() ��x��
��x��![]() ��
��
��2��.������������ۼ��ɣ���Բ����A�� CA=3ʱ����Բ��СԲ����ʱ����Բ���� A��AC=1ʱ����Բ���� B ʱ�����ɵó�.
���������
��1��![]() ��
��
��![]() ��ѵ���С����Ϊ
��ѵ���С����Ϊ![]() ����
����![]() ��ѵ���С����Ϊ1����
��ѵ���С����Ϊ1����![]() ��ѵ���С����Ϊ
��ѵ���С����Ϊ![]() ��
��
��ѵĹ�����Ϊ![]() ��
��![]() ��
��
�ڸ��ݶ���������ɵõ�ֱ��y=-x�ϵĵ�P��ԭ��ľ�����1��3֮��ʱ�������⣻
�� ���P������ΪP (x ��-x) ��
��OP=1ʱ���ɾ��빫ʽ�ɵã�OP=![]() �����
�����![]() ����OP=3ʱ���ɾ��빫ʽ�ɵã�OP=
����OP=3ʱ���ɾ��빫ʽ�ɵã�OP=![]() ��
��![]() �����
�����![]() ��
��
�� ��ĺ������ȡֵ��ΧΪ��![]() ��x�ܣ�
��x�ܣ�![]() ��
��![]() ��x��
��x��![]()
��2����y=-x+1���ᡢ��Ľ���ֱ�ΪA��B���㣬�� ��y=0�ã�-x+1=0�����x=1��
���x=0����y=0��
��A(1��0) ��B (0��1) ��
�����ã�
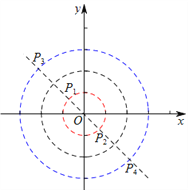
��ͼ1����Բ����Aʱ����ʱCA=3��
�� ��C������C ( -2��0)

��ͼ2����Բ��СԲ����ʱ���е�ΪD��
��CD=1 ��
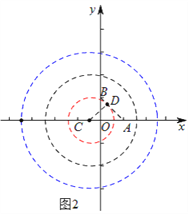
�֡�ֱ��AB���ڵĺ�������ʽΪy=-x+1��
�� ֱ��AB��x���γɵļн���45�㣬
�� RT��ACD��CA=![]() ��
��
�� C������Ϊ (1-![]() ��0)
��0)
�� C��ĺ������ȡֵ��ΧΪ��-2��![]() ��1-
��1-![]() ��
��
��ͼ3����Բ����Aʱ��AC=1��
C������Ϊ(2��0)

��ͼ4��
��Բ���� B ʱ������ BC ����ʱ BC =3��
�� Rt��OCB�У��ɹ��ɶ�����OC=![]() �� C������Ϊ (2
�� C������Ϊ (2![]() ��0)��
��0)��
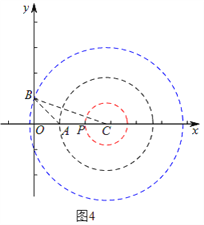
�� C��ĺ������ȡֵ��ΧΪ2��![]() ��2
��2![]() ��
��
������������C�ĺ������ȡֵ��ΧΪ��![]() ��
��![]() �ܣ�
�ܣ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��


 ������ϰ�ο����뵥Ԫ���ϵ�д�
������ϰ�ο����뵥Ԫ���ϵ�д� �����Ծ���ĩ���100��ϵ�д�
�����Ծ���ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=ax2+bx+c��x�ύ��A��B���㣬����C��������Ϊ��2���ֽ�����������ƽ��2����λ���õ�������y=a1x2+b1x+c1�������н�����ȷ���� ����д��������ȷ���۵���ţ�
��b��0
��a��b+c��0
����Ӱ���ֵ����Ϊ4
����c=��1����b2=4a��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ȤС��Ϊ�˽��������±仯�������¼�˽����·�����![]() ���������£���λ��������
���������£���λ��������![]() .�����������ݣ����н��۲���ȷ���ǣ� ��
.�����������ݣ����н��۲���ȷ���ǣ� ��
A��ƽ������![]() B����λ����
B�������![]() C.������
C.������![]() D��������
D��������![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
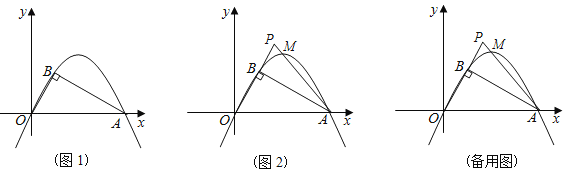
����Ŀ����ͼ1��������y��ax2+bx����ԭ��O�͵�A��12��0������B���������ϣ���֪OB��BA���ҡ�A��30�㣮
��1����������ߵĽ���ʽ��
��2����ͼ2����PΪOB�ӳ�����һ�㣬������AP���������ڵ�M�����P�ĺ�����Ϊt����M�ĺ�����Ϊm�����ú���t�Ĵ���ʽ��ʾm����Ҫ��дȡֵ��Χ��
��3���ڣ�2���������£�����O��OW��AP��W�������߶�AB�ڵ�G������W��ֱ�߽�OP�ӳ����ڵ�N����x���ڵ�K������WKA��2��OAP����NK��11�����M�ĺ����꼰WG�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ǽס�����������˶�Ա��10��������Գɼ�������ͳ��ͼ.
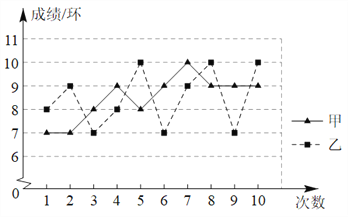
��1����������ͼ�����б���������
�˶�Ա | ƽ���� | ��λ�� | ���� |
�� | 8.5 | 9 | |
�� | 8.5 |
��2����������ͼ��������ѧͳ��֪ʶ�Լס��������˶�Ա�����ˮƽ�������۲�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���׳���![]() �س�������ʻ��
�س�������ʻ��![]() �أ�����
�أ�����![]() �غ�������ԭ·ԭ�ٷ���
�غ�������ԭ·ԭ�ٷ���![]() �أ��ҳ���
�أ��ҳ���![]() �س�������ͬ·������ʻ��
�س�������ͬ·������ʻ��![]() �أ�����
�أ�����![]() Сʱ���ҳ��������;��ͣ��
Сʱ���ҳ��������;��ͣ��![]() Сʱ��Ȼ�������ԭ��ʻ��
Сʱ��Ȼ�������ԭ��ʻ��![]() �أ��ҳ�����ʻ�����е��ٶ���
�أ��ҳ�����ʻ�����е��ٶ���![]() ǧ��/ʱ���׳����ҳ���
ǧ��/ʱ���׳����ҳ���![]() Сʱ����
Сʱ����![]() �أ���������Գ����ص�·��
�أ���������Գ����ص�·��![]() ǧ����׳���ʻʱ��
ǧ����׳���ʻʱ��![]() Сʱ֮��ĺ�����ϵ��ͼ��ʾ������ͼ����Ϣ����������⣺
Сʱ֮��ĺ�����ϵ��ͼ��ʾ������ͼ����Ϣ����������⣺
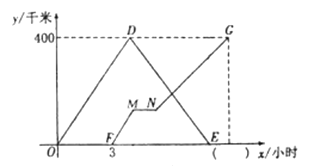
��1��д���׳���ʻ���ٶȣ���ֱ��д��ͼ����������ȷ����__ __
��2����׳���![]() �ط���
�ط���![]() �صĹ����У�
�صĹ����У�![]() ��
��![]() �ĺ�����ϵʽ(����Ҫд���Ա���
�ĺ�����ϵʽ(����Ҫд���Ա���![]() ��ȡֵ��Χ)��
��ȡֵ��Χ)��
��3��ֱ��д���׳���������Сʱ������ǡ�����![]() ǧ�ף�
ǧ�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
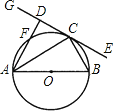
����Ŀ����ͼ����O��ֱ��AB��6��CΪԲ���ϵ�һ�㣬BC��3����C������O������GE����AD��GE�ڵ�D������O�ڵ�F��
��1����֤����ACG����B��
��2�������߶�AF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���x2����m��2��x����2m��1��=0��
��1����֤�����̺�����������ȵ�ʵ������
��2�����˷��̵�һ������1����������̵���һ�����������Դ�����Ϊ�߳���ֱ�������ε��ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����һ�����Ƴ�����ƽ��ÿ����۳�20����ÿ��Ӯ��40Ԫ��Ϊ���������ۣ�����Ӯ����������ٿ�棬�̳�������ȡ�ʵ��Ľ��۴�ʩ�������鷢�֣����ÿ������ÿ����1Ԫ���̳�ƽ��ÿ��ɶ��۳�2������
��1�����̳�ƽ��ÿ��ҪӮ��1200Ԫ��ÿ������Ӧ���۶���Ԫ��
��2��ÿ���������۶���Ԫʱ���̳�ƽ��ÿ��Ӯ����ࣿ
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com