

���� ��1���������߽���ʽ��õ�A��C�����꣬Ȼ����ݴ���ϵ��������ֱ��AC��ֱ�߷��̼��ɣ�
��2�����ͼ2����ֱ��������AOC�����ù��ɶ������AC�ij��ȣ�����D��DI��AC�ڵ�I������ȫ�������Ρ�ADI�ա�ADO��SSA����Rt��CDI������ȫ�������ε����ʿ�����DI=DO=m����DC=OC-OD=4-m�����Ը��ݹ��ɶ����г�����m�ķ��̣������ڷ��̽��⼴����õ�D�����ꣻȻ�����ô���ϵ�������ֱ��AD���̣���ֱ���ϵ�����������������ε������ʽ�Ͷ��κ�����ֵ���������BEF��������ֵ�ʹ�ʱ��P�����ꣻ������ƽ�Ƶ����ʣ�����������߶����ȷ��W��·������Сֵ��
��3����Ҫ�������ۣ��ٵ�����G���߶�BC��ʱ�����ͼ3����P��t��0��������취�г��������t���Ӷ���õ�P������������εı߳�����ʱ�ص������ǡ�EHM���ڵ�����H���߶�BC��ʱ�����ͼ4���ص��������ı���EHNQ������S=S��EHQ+S��HNQ��⼴�ɣ�
��� �⣺��1�����ͼ1��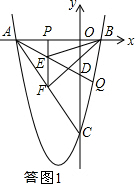
�����ߵĽ���ʽΪ��y=$\frac{4}{3}$x2+$\frac{8}{3}$x-4��
��x=0����y=-4��
��C��0��-4����
��y=0���� $\frac{4}{3}$x2+$\frac{8}{3}$x-4=0��
��ã�x1=-3��x2=1��
��A��-3��0����B��1��0����
��ֱ��AC����ֱ�߽���ʽΪ��y=kx+b��k��0����
��A��-3��0����C��0��-4������ɵã�$\left\{\begin{array}{l}{-3k+b=0}\\{b=-4}\end{array}\right.$��
��� $\left\{\begin{array}{l}{k=-\frac{4}{3}}\\{b=-4}\end{array}\right.$��
ֱ��AC����ֱ�߽���ʽΪ��y=-$\frac{4}{3}$x-4��
��2������D��DI��AC�ڵ�I�����ͼ2��
��A��-3��0����C��0��-4����
��OA=3��
��OC=4��
��Rt��AOC��AC=$\sqrt{O{A}^{2}+O{C}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5��
���ڡ�ADI���ADO�У�
$\left\{\begin{array}{l}{��DIA=��DOA=90��}\\{��DAI=��DAO}\\{DA=DA}\end{array}\right.$��
���ADI�ա�ADO��SSA����
��AI=AO=3��DI=DO��
��DI=DO=m����DC=OC-OD=4-m��
��IC=AC-AI��
��IC=5-3=2��
��Rt��CDI����ID2+IC2=DC2��
��m2+22=��4-m��2��
��ã�m=$\frac{3}{2}$��
��OD=$\frac{3}{2}$��
��D��0��-$\frac{3}{2}$����
��ֱ��AD����ֱ�߽���ʽΪ��y=kx+b��k��0����
��A��-3��0����D��0��-$\frac{3}{2}$������ɵã�$\left\{\begin{array}{l}{-3k+b=0}\\{b=-\frac{3}{2}}\end{array}\right.$��
��� $\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=-\frac{3}{2}}\end{array}\right.$��
ֱ��AD����ֱ�߽���ʽΪ��y=-$\frac{1}{2}$x-$\frac{3}{2}$��
�֡�ֱ��AC�Ľ���ʽΪ��y=-$\frac{4}{3}$x-4��
����P��n��0������E��n��-$\frac{1}{2}$n-$\frac{3}{2}$����F��n��-$\frac{4}{3}$n-4����
��BP=1-n��EF=��-$\frac{1}{2}$n-$\frac{3}{2}$��-��-$\frac{4}{3}$n-4��=$\frac{5}{6}$n+$\frac{5}{2}$��
��S��BEF=$\frac{1}{2}$EF•BP=$\frac{1}{2}$�� $\frac{5}{6}$n+$\frac{5}{2}$����1-n��=-$\frac{5}{12}$n2-$\frac{5}{6}$n+$\frac{5}{4}$��-3��n��1����
��ú����ĶԳ�����ֱ��x=-1��
�൱x=-1ʱ��S��BEF�����ֵ=$\frac{5}{3}$��
��ʱ��P��-1��0����E��-1��-1����F��-1��-$\frac{8}{3}$����
��EF=$\frac{8}{3}$-1=$\frac{5}{3}$��
��BB���EF��BB��=EF������CB�佻FJ��M����MN��EK��N������BN����W���������·��B��N��M��C������ͼ2���к�ɫ�ߣ���
���·����=BN+MN+CM=B��M+CM+EF=CB��+EF=$\frac{5}{3}$+$\frac{\sqrt{58}}{3}$��
��3����B��1��0����C��0��-4���ɵ�ֱ��BC�Ľ���ʽΪ��y=4x-4��
�ٵ�����G���߶�BC��ʱ�����ͼ3���ص������ǡ�EHM��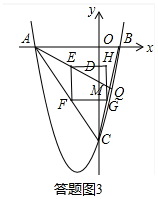
��P��t��0������E��t��-$\frac{1}{2}$t-$\frac{3}{2}$����F��t��-$\frac{4}{3}$t-4����G��-$\frac{1}{3}$t��-$\frac{4}{3}$t-4����
��EF=��-$\frac{1}{2}$t-$\frac{3}{2}$��-��-$\frac{4}{3}$t-4��=$\frac{6}{5}$t+$\frac{5}{2}$��FG=-$\frac{1}{3}$t-t=-$\frac{4}{3}$t��
��EF=FG��
��$\frac{5}{6}$t+$\frac{5}{2}$=-$\frac{4}{3}$t��
��ã�t=-$\frac{15}{13}$��
��FG=-$\frac{4}{3}$����-$\frac{15}{13}$��=$\frac{20}{13}$��
�ඥ��G���߶�BC��ʱ��P��-$\frac{15}{13}$��0���������εı߳�Ϊ $\frac{20}{13}$��G��$\frac{5}{13}$��-$\frac{32}{13}$����M��$\frac{5}{13}$��-$\frac{22}{13}$����
��HM=$\frac{10}{13}$��EH=$\frac{20}{13}$��
��S=$\frac{1}{2}$•$\frac{10}{13}$•$\frac{20}{13}$=$\frac{100}{169}$��
�ڵ�����H���߶�BC��ʱ�����ͼ4���ص��������ı���EHNQ��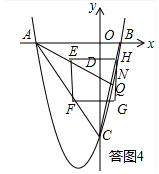
��P��t��0������E��t��-$\frac{1}{2}$t-$\frac{3}{2}$����F��t��-$\frac{4}{3}$t-4����H��-$\frac{1}{8}$t+$\frac{5}{8}$��-$\frac{1}{2}$t-$\frac{3}{2}$����
��EF=��-$\frac{1}{2}$t-$\frac{3}{2}$��-��-$\frac{4}{3}$t-4��=$\frac{5}{6}$t+$\frac{5}{2}$��EH=��-$\frac{1}{8}$t+$\frac{5}{8}$��-t=-$\frac{9}{8}$t+$\frac{5}{8}$��
��EF=EH��
��$\frac{5}{6}$t+$\frac{5}{2}$=-$\frac{9}{8}$t+$\frac{5}{8}$��
��ã�t=-$\frac{45}{47}$��
��EF=$\frac{5}{6}$����-$\frac{45}{47}$��+$\frac{5}{2}$=$\frac{80}{47}$��
�ඥ��H���߶�BC��ʱ��P��-$\frac{45}{47}$��0����E��-$\frac{45}{47}$��-$\frac{48}{47}$����H��$\frac{35}{47}$��-$\frac{48}{47}$���������εı߳�Ϊ $\frac{80}{47}$��
��AC�Ľ���ʽΪy=-$\frac{1}{2}$x-$\frac{3}{2}$��
��$\left\{\begin{array}{l}{y=-\frac{1}{2}x-\frac{3}{2}}\\{y=\frac{4}{3}{x}^{2}+\frac{8}{3}x-4}\end{array}\right.$���$\left\{\begin{array}{l}{x=-3}\\{y=0}\end{array}\right.$��$\left\{\begin{array}{l}{x=\frac{5}{8}}\\{y=-\frac{29}{16}}\end{array}\right.$��
���Q��$\frac{5}{8}$��-$\frac{29}{16}$����
��ֱ��BQ����ʽΪy=$\frac{29}{6}$x-$\frac{29}{6}$��
��N��$\frac{35}{47}$��-$\frac{58}{47}$��
��S=S��EHQ+S��HNQ=$\frac{1}{2}$•��$\frac{35}{47}$+$\frac{45}{47}$��•��$\frac{29}{16}$-$\frac{48}{47}$��+$\frac{1}{2}$•��$\frac{35}{47}$-$\frac{5}{8}$��•��$\frac{58}{47}$-$\frac{48}{47}$��=$\frac{12125}{17672}$��
��������������G���߶�BC��ʱ���ص��������Ϊ$\frac{100}{169}$������H���߶�BC��ʱ���ص��������Ϊ$\frac{12125}{17672}$��
���� ���⿼���˶��κ����ۺ��⣬�����漰���˴���ϵ������һ�κ�������ʽ������ͼ���ϵ���������������κ�����ֵ�������ɶ����Լ������ε����ʣ������ѶȽϴ����й��ڶ�������Ľ��ʱ���м�Ҫ�������ۣ��Է�©�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
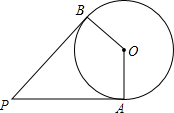 ��ͼ��PA��PB�ǡ�O�����ߣ�A��BΪ�е㣬��OA=2����P=60�㣬��$\widehat{AB}$�ij�Ϊ��������
��ͼ��PA��PB�ǡ�O�����ߣ�A��BΪ�е㣬��OA=2����P=60�㣬��$\widehat{AB}$�ij�Ϊ��������| A�� | $\frac{2}{3}$�� | B�� | $\frac{4}{3}��$ | C�� | $\frac{1}{3}��$ | D�� | $\frac{5}{3}��$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{12}$ | B�� | $\sqrt{\frac{2}{3}}$ | C�� | $\sqrt{60}$ | D�� | $\sqrt{18}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com