
| 3 |
| 2 |
| 1-2c |
| 2 |
| 1-2c |
| 2 |
| 3 |
| 2 |
| 1-2c |
| 2 |
| 1-2c |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| m |
| 2 |
| m |
| 2 |
| 6-c |
| 2 |
| 6-c |
| 2 |
| 6-c |
| 2 |
| 6-c |
| 2 |
| 6-c |
| 2 |
| 6-c |
| 2 |


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:阅读理解
| 3 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 9 |
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1-2c |
| 2 |
| 1-2c |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1-2c |
| 2 |
| 1-2c |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| m |
| 2 |
| m |
| 2 |
查看答案和解析>>
科目:初中数学 来源:藁城市一模 题型:解答题
| 3 |
| 2 |
| 1-2c |
| 2 |
| 1-2c |
| 2 |
| 3 |
| 2 |
| 1-2c |
| 2 |
| 1-2c |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| m |
| 2 |
| m |
| 2 |
查看答案和解析>>
科目:初中数学 来源:2010年河北省石家庄市藁城市中考数学一模试卷(解析版) 题型:解答题
 ,求a,b,c的值.
,求a,b,c的值. ①
① ②
②
 .∴
.∴ .
. ,合理运用这种换元技巧,可顺利解决一些问题.现请你根据上述方法试解决下面问题:
,合理运用这种换元技巧,可顺利解决一些问题.现请你根据上述方法试解决下面问题:查看答案和解析>>
科目:初中数学 来源:2002年湖北省荆门市中考数学试卷(解析版) 题型:解答题
 =0,求a、b、c的值.
=0,求a、b、c的值. =0.②
=0.② =0.∴ab=2c2+c+
=0.∴ab=2c2+c+ ③
③ =0④的两个实数根.
=0④的两个实数根. ≥0,即(c+1)2≤0.而(c+1)2≥0,∴c+l=0,c=-1,
≥0,即(c+1)2≤0.而(c+1)2≥0,∴c+l=0,c=-1, =0.∴t1=t2=
=0.∴t1=t2= ,即a=b=
,即a=b= .∴a=b,c=-1.
.∴a=b,c=-1. +t,b=
+t,b= -t.①
-t.① =0,∴(a+b)2-2ab+6c+
=0,∴(a+b)2-2ab+6c+ =0.②
=0.② +6c+
+6c+ =0.
=0. ,b=
,b= .a=b=
.a=b= ,c=-1.
,c=-1. +t,y=
+t,y=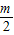 -t.一些问题根据条件,若合理运用这种换元技巧,则能使问题顺利解决.
-t.一些问题根据条件,若合理运用这种换元技巧,则能使问题顺利解决.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com