
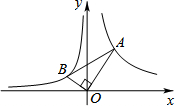
 如图,已知第一象限内的点A在反比例函y=$\frac{4}{x}$上,第二象限的点B在反比例函数y=$\frac{k}{x}$上,且OA⊥OB,tanA=$\frac{1}{2}$,则k的值为-1.
如图,已知第一象限内的点A在反比例函y=$\frac{4}{x}$上,第二象限的点B在反比例函数y=$\frac{k}{x}$上,且OA⊥OB,tanA=$\frac{1}{2}$,则k的值为-1. 分析 作AC⊥x轴于点C,作BD⊥x轴于点D,易证△OBD∽△AOC,则面积的比等于相似比的平方,即tanA的平方,然后根据反比例函数中比例系数k的几何意义即可求解.
解答 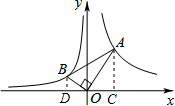 解:作AC⊥x轴于点C,作BD⊥x轴于点D.
解:作AC⊥x轴于点C,作BD⊥x轴于点D.
则∠BDO=∠ACO=90°,
则∠BOD+∠OBD=90°,
∵OA⊥OB,
∴∠BOD+∠AOC=90°,
∴∠BOD=∠AOC,
∴△OBD∽△AOC,
∴$\frac{{S}_{△OBD}}{{S}_{△AOC}}$=($\frac{OB}{OA}$)2=(tanA)2=$\frac{1}{4}$,
又∵S△AOC=$\frac{1}{2}$×4=2,
∴S△OBD=$\frac{1}{2}$,
∴k=-1.
故答案为:-1.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
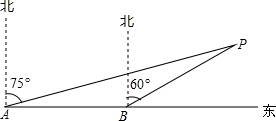 如图所示,为了躲避海盗,一轮船由西向东航行,早上8点,在A处测得小岛P在北偏东75°的方向上,以每小时20海里的速度继续向东航行,10点到达B处,并测得小岛P在北偏东60°的方向上,已知小岛周围25海里内有暗礁,若轮船仍向前航行,有无触礁的危险?你对船长有何建议?
如图所示,为了躲避海盗,一轮船由西向东航行,早上8点,在A处测得小岛P在北偏东75°的方向上,以每小时20海里的速度继续向东航行,10点到达B处,并测得小岛P在北偏东60°的方向上,已知小岛周围25海里内有暗礁,若轮船仍向前航行,有无触礁的危险?你对船长有何建议?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
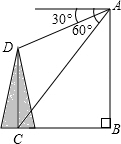 如图,在200米高的峭壁上,测得一塔的塔顶与塔基的俯角分别为30°和60°,那么塔高是( )米.
如图,在200米高的峭壁上,测得一塔的塔顶与塔基的俯角分别为30°和60°,那么塔高是( )米.| A. | $\frac{200}{3}$ | B. | $\frac{400}{3}$ | C. | $\frac{500}{3}$ | D. | $\frac{700}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
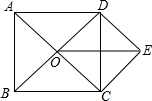 如图:O是矩形ABCD对角线AC、BD的交点,过点D作DE∥AC,过点C作CE∥BD,DE、CE相交于点E,连结OE交CD于点F,那么OE与DC垂直吗?请说明理由.
如图:O是矩形ABCD对角线AC、BD的交点,过点D作DE∥AC,过点C作CE∥BD,DE、CE相交于点E,连结OE交CD于点F,那么OE与DC垂直吗?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
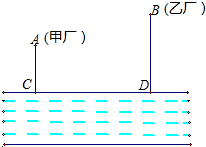 如图,在河流的一侧有甲、乙两个工厂,它们各有一条垂直于江边的小路,长度分别为4千米和5千米,若两条小路相距18千米,现要在江边建立一个抽水站,把水送到甲、乙两厂去,要使供水管长度之和最短,抽水站应建在哪里?
如图,在河流的一侧有甲、乙两个工厂,它们各有一条垂直于江边的小路,长度分别为4千米和5千米,若两条小路相距18千米,现要在江边建立一个抽水站,把水送到甲、乙两厂去,要使供水管长度之和最短,抽水站应建在哪里?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
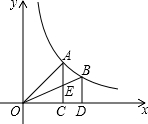 如图,过反比例函数y=$\frac{3}{x}$(x>0)图象上任意两点A、B分别作x轴的垂线,垂足为C、D,连接OA、OB.设AC与OB的交点为E,△AOE与梯形ECDB的面积分别为S1、S2,则( )
如图,过反比例函数y=$\frac{3}{x}$(x>0)图象上任意两点A、B分别作x轴的垂线,垂足为C、D,连接OA、OB.设AC与OB的交点为E,△AOE与梯形ECDB的面积分别为S1、S2,则( )| A. | S1>S2 | B. | S1=S2 | ||
| C. | S1<S2 | D. | S1、S2的大小关系不确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 方程两根之和是1 | B. | 方程两根之积是3 | ||
| C. | 方程两根之平方和是7 | D. | 方程两根倒数之和是3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com