C
分析:①由于以A为顶点的角有几个,可以分别以AB为一边,分别取AC、AD、AE作为一边,由此即可得到以A为顶点的角的个数;
②图中互补的角就是分别以C、D为顶点的两对邻补角,由此即可确定选择项;
③由于∠BAE=m°,∠CAD=n°,根据图形不能确定∠BAC-∠DAE等于多少,所以不能判定;
④由于BC=11,BD:CE=2:l,DE=

BD+3,由此可以分别求出CD、DE的长度,而所求三角形是等高的,由此即可判定选择项.
解答:①A为顶点的角有6个,分别是∠BAC、∠BAD、∠BAE、∠CAD、∠CAE、∠DAE,故选项正确;
②图中互补的角就是分别以C、D为顶点的两对邻补角,即∠BCA和∠ACD互补,∠ADE和∠ADC互补,故选项正确;
③∵∠BAE=m°,∠CAD=n°,根据图形可以求出∠BAC+∠DAE=(m+n)°,不能求出∠BAC-∠DAE=(m+n)°故选项不正确;
④∵BC=BD+DE+CE=11 ①,BD:CE=2:l,设CE=x,那么BD=2x,而DE=

BD+3=

x+3,分别把BD、DE、CE代入①即可得:x=2,∴BD=4,DE=5,CE=2,∴S
△ABD:S
△ADE:S
△ACE=4:5:2,故选项正确.
故选C.
点评:此题分别考查了三角形的面积公式、三角形的中线、高线、角平分线的性质,难度不大,都是基础知识,对于学生要求熟练掌握这些基础知识.

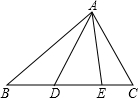 如图,D、E在线段BC上.下列说法:①以A为顶点的角共有6个:②图中有2对互补的角;③若∠BAE=m°,∠CAD=n°,则∠BAC-∠DAE=(m+n)°;④若BC=11,BD:CE=2:l,DE=
如图,D、E在线段BC上.下列说法:①以A为顶点的角共有6个:②图中有2对互补的角;③若∠BAE=m°,∠CAD=n°,则∠BAC-∠DAE=(m+n)°;④若BC=11,BD:CE=2:l,DE= BD+3,则S△ABD:S△ADE:S△ACE=4:5:2.其中说法正确的是
BD+3,则S△ABD:S△ADE:S△ACE=4:5:2.其中说法正确的是 BD+3,由此可以分别求出CD、DE的长度,而所求三角形是等高的,由此即可判定选择项.
BD+3,由此可以分别求出CD、DE的长度,而所求三角形是等高的,由此即可判定选择项. BD+3=
BD+3= x+3,分别把BD、DE、CE代入①即可得:x=2,∴BD=4,DE=5,CE=2,∴S△ABD:S△ADE:S△ACE=4:5:2,故选项正确.
x+3,分别把BD、DE、CE代入①即可得:x=2,∴BD=4,DE=5,CE=2,∴S△ABD:S△ADE:S△ACE=4:5:2,故选项正确.

 发散思维新课堂系列答案
发散思维新课堂系列答案