Question

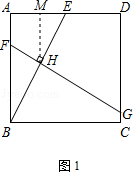
正方形ABCD中，E为AD上的一点（不与A、D点重合），AD=nAE，BE的垂直平分线分别交AB、CD于F、G两点，垂足为H．
（1）如图1，当n=2时，则=　_________　；
（2）如图1，当n=2时，求的值；
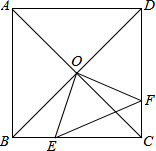
（3）延长FG交BC的延长线于M（如图2），直接填空：当n=　_________　时，．

Answer 1

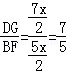（1）    （2）     （3）

解析试题分析：（1）如图1，过点H作HM⊥AD于M．
∵BE的垂直平分线分别交AB、CD于F、G两点，HM⊥AD，
∴MH是△ABE的中位线，
∴AM=ME；
∵AD=2AE，
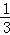∴AM=DM，
∴==（平行线分线段成比例定理），
故答案为：；
（2）如图2，连接EG、BG．
∵ABCD是正方形，
∴AB=BC=CD=AD，∠A=∠D=∠C=90°．
设AB=BC=CD=AD=4x，CG=y．
当n=2时，AD=2AE，
∴AE=ED=2x；
在Rt△EDG中，EG²=ED²+DG²（勾股定理），
即EG²=（2x）²+（4x﹣y）²．
在Rt△BCG中，BG²=BC²+CG²，
即BG²=（4x）²+y²．
∵FG垂直平分BE，
∴EG=BG．
∴（2x）²+（4x﹣y）²=（4x）²+y²
得y=，
∴DG=DC﹣CG=．
∵FH⊥BE，
∴∠BHF=90°
可得Rt△BHF∽Rt△BAE，可得BF=．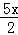
∴；
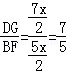（3）n=．



考点：相似形综合题；勾股定理；正方形的性质；相似三角形的判定与性质．
点评：本题综合考查了正方形的性质、相似三角形的判定与性质以及勾股定理等知识点．要充分利用好正方形的性质，通过已知和所求的条件构建出相似三角形来求解是解题的关键．