
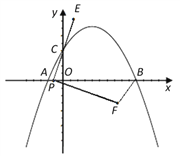
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��A��B��C������ֱ�Ϊ(-1��0)��(5��0)��(0��2)��
��1�����A��B��C����������߽���ʽ��
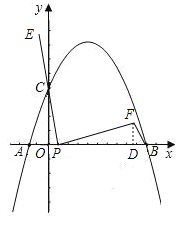
��2������P��A���������x����������ÿ��1����λ���ȵ��ٶ���B���ƶ�������PC���ӳ�����E��ʹCE=PC�����߶�PE�Ƶ�P˳ʱ����ת90��õ��߶�PF������FB������P�˶���ʱ��Ϊt��(0��t��6)�����PBF�����ΪS��
����S��t�ĺ�����ϵʽ��
�ڵ�t�Ƕ���ʱ����PBF���������������Ƕ��٣�
��3����P���ƶ��Ĺ����У���PBF�ܷ��Ϊֱ�������Σ����ܣ�ֱ��д����F�����ꣻ�����ܣ���˵�����ɣ�
���𰸡���1��![]() ;��2���� S��PBF=t2��7t+6��0��t��1��,S��PBF=��t2+7t��6��1��t��6������
;��2���� S��PBF=t2��7t+6��0��t��1��,S��PBF=��t2+7t��6��1��t��6������
��t=3.5ʱ�������������ֵΪ6.25;��3����,F������Ϊ����5�� ![]() ����5��2����
����5��2����
����������������1����Ϊ�����߹�A��B��C���㣬���Դ����������ʹ�����ߵĽ���ʽ��������2���ٴ���Ҫ������������������ۣ�
һ����P��λ��ԭ����࣬�߶�OA�ϣ���ʱ0��t<1������t��ʾ��OP��BP�ij��������BPF��������ؼ�Ҫ���BP���ϵĸߣ��ɹ�F��FD��x����D�����ڡ�CPF=90�㣬��֤����OPC�ס�DFP��������֪������֪PF=PE=2PC�����������������ε����Ʊ�Ϊ2����ôDF=2OP���ɴ˿ɵõ�DF�ij�����BPΪ�ף�DFΪ�ߣ�������á�BPF���������ʽ��Ҳ�͵õ��˹���S��t�ĺ�����ϵʽ��
������P��λ��ԭ���Ҳ࣬�߶�BP�ϣ���ʱ1<t<6���ɷ���һ�ķ���������⣻
�ڸ��ݢٵõ���S��t�ĺ�����ϵʽ������Ӧ���Ա�����ȡֵ��Χ�����ɸ��ݺ������������S�����ֵ����Ӧ��tֵ��Ȼ����бȽϼ��ɵõ������
��3����Pλ���߶�OA��ʱ����Ȼ��PFB��������ֱ�������Σ����ڡ�BPF<��CPF=90�㣬����P��������ֱ�Ƕ��㣬�ɷ���������������ۣ�
��FΪֱ�Ƕ��㣬��F��FD��x����D���ɣ�2����֪BP=6-t��DP=2OC=4����Rt��OCP�У�OP=t-1���ɹ��ɶ��������CP=t2-2t+5����ôPF=![]() =4��t-2t+5������Rt��PFB�У�FD��PB������Ӱ���������PB=PF��PD=t-2t+5����PB����һ������ʽΪ��PB=6-t��������ʽ�ɵ�t-2t+5=6-t����t=
=4��t-2t+5������Rt��PFB�У�FD��PB������Ӱ���������PB=PF��PD=t-2t+5����PB����һ������ʽΪ��PB=6-t��������ʽ�ɵ�t-2t+5=6-t����t=![]() ��
��
��BΪֱ�Ƕ��㣬��ô��ʱ������루2�������ƣ���PFB�ס�CPO�������Ʊ�Ϊ2����ôBP=2OC=4����OP=OB-BP=1����ʱt=2��
�����������1������һ���������ߵĽ���ʽΪy=ax2+bx+c��a��0����
��A����1��0����B��5��0����C��0��2��
����������ʽ�ã� 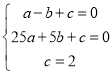 �� ���
�� ���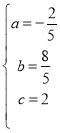
��![]() ��
��
���������������ߵĽ���ʽΪy=a��x��5����x+1����
�ѣ�0��2���������ʽ�ã�2=��5a��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��2���ٹ���F��FD��x����D��
����P��ԭ�����ʱ��BP=6��t��OP=1��t��
��Rt��POC�У���PCO+��CPO=90�㣬
���FPD+��CPO=90�㣬
�ߡ�PCO=��FPD��
���POC=��FDP��
���CPO�ס�PFD��
��![]()
��PF=PE=2PC��
��FD=2PO=2��1��t����
��S��PBF= ![]() =t2��7t+6��0��t��1����
=t2��7t+6��0��t��1����
����P��ԭ���Ҳ�ʱ��OP=t��1��BP=6��t��
�ߡ�CPO�ס�PFD��
��FD=2��t��1������S��PBF= ![]() =��t2+7t��6��1��t��6����
=��t2+7t��6��1��t��6����
�ڵ�0��t��1ʱ��S=t2��7t+6��
��ʱt��t=3.5����࣬S��t���������С��
���У���t=0ʱ��Smax=0��7��0+6=6��
��1��t��6ʱ��S=��t2+7t��6��
����1��3.5��6���ʵ�t=3.5ʱ��Smax=��3.5��3.5+7��3.5+6=6.25��
������������t=3.5ʱ�������������ֵΪ6.25��
��3���ܣ�����FΪֱ�Ƕ��㣬��F��FD��x����D��
�ɣ�2����֪BP=6��t��DP=2OC=4��
��Rt��OCP��OP=t��1��
�ɹ��ɶ��������CP2=t2��2t+5��
��ôPF
��Rt��PFB��FD��PB��
����Ӱ���������PB=PF2��PD=t2��2t+5��
��PB����һ������ʽΪ��PB=6��t��
������ʽ�ɵ�t2��2t+5=6��t��
��t=![]() ��P��������
��P��������![]() ��0����
��0����
��F����������5�� ![]() ����
����
��BΪֱ�Ƕ��㣬��ô��ʱ������루2�������ƣ���PFB�ס�CPO�������Ʊ�Ϊ2��
��ôBP=2OC=4����OP=OB��BP=1����ʱt=2��P������Ϊ��1��0����FD=2��t��1��=2��
��F��������5��2����


 �������Ӧ���⼯ѵϵ�д�
�������Ӧ���⼯ѵϵ�д� �ۺ��Բ�ϵ�д�
�ۺ��Բ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��˵���������������������ϵĸ�С�������Ǽ����⣬�����ҵķ�����_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����(x+2y)(2x-ky-1)�Ľ���в���xy���k��ֵΪ�� ��
A. 4 B. -4 C. 2 D. -2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
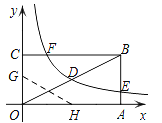
����Ŀ����ͼ������OABC�Ķ���A��C�ֱ���x��y����������ϣ���DΪ�Խ���OB���е㣬��E��8��n���ڱ�AB�ϣ�����������![]() ��k��0���ڵ�һ�����ڵ�ͼ����D��E����tan��BOA=
��k��0���ڵ�һ�����ڵ�ͼ����D��E����tan��BOA=![]() ��
��
��1�����������Ľ���ʽ��n��ֵ��
��2����������������ͼ������εı�BC���ڵ�F���������۵���ʹ��O���F�غϣ��ۺ۷ֱ���x��y�������ύ�ڵ�H��G����G������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ÿ���Ա�������ٰ���˫ʮһ�������������̼Ҷ�����������������д��������Ĵ����������������һ��A��Ʒ�ɱ�Ϊ50Ԫ�����ϱ��80Ԫ��
��1����˫ʮһ���������죬�������������ν�������A��Ʒ������������ƽ��ÿ�ν�����Ϊ���٣�����ʹ���A��Ʒ��������Ϊ10%�����ο����ݣ� ![]() ��0.83��
��0.83��![]() ��0.64��
��0.64��![]() ��1.05��
��1.05��
��2����ý�屬�ϣ���һЩ�Ա��̼�����˫ʮһ���������죬�������Ʒ�����ϱ�ۺ����Ƴ��������������թ��Ϊ����˫ʮһ���֮ǰ������������A��Ʒ�ijɱ������ϱ���������һ�£�һ�ܿ��۳�60��A��Ʒ������˫ʮһ���������죬�������Ƚ����ϱ�����a%�����Ƴ��������۵Ĵ�����������˴��������ߣ�����������˫ʮһ����������������A��Ʒ����Ҳ��ԭ��һ��������A��Ʒ����������a%��������˫ʮһ������������������ﵽ��3600Ԫ��������������˫ʮһ��������������ϱ��Ϊ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����y����ax2+bx+c��ͼ�ڷ������ϣ���a_____0����������������������գ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y��ax2+bx+c������A����3��0����B��1��0����C��0��3������������ߵĽ���ʽ��д�����ĶԳ���Ͷ������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У��㣨1��1������y��ԳƵĵ��������
A. ��-1��-1�� B. ��1��-1�� C. ��-1��1�� D. ��1��1��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com