
 ,∠CAD=30°.
,∠CAD=30°.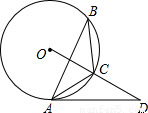
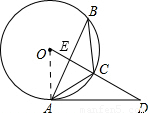
 ,那么可求∠B=30°,利用圆周角定理可求∠AOC=60°,而OA=OB,那么△AOC是等边三角形,从而有∠OAC=60°,易求∠OAD=90°,即AD是⊙O的切线;
,那么可求∠B=30°,利用圆周角定理可求∠AOC=60°,而OA=OB,那么△AOC是等边三角形,从而有∠OAC=60°,易求∠OAD=90°,即AD是⊙O的切线; ,
,
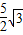 ,
, .
.

科目:初中数学 来源: 题型:
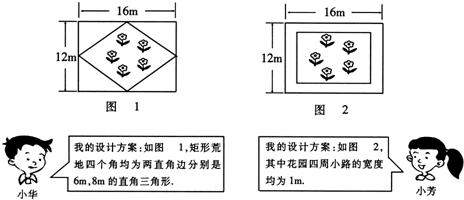
查看答案和解析>>
科目:初中数学 来源:2010年广东省中考数学全真模拟试卷(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2009年江苏省宿迁市泗洪县中考数学模拟试卷(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com