
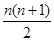 ,25,n2;
,25,n2;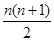 ,25,n2;
,25,n2; ,
,
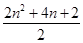
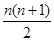 ,25,n2;25=10+15,36=15+21.
,25,n2;25=10+15,36=15+21.

 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源:不详 题型:解答题
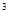 -6a
-6a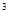 b+3a
b+3a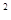 b)-(-3a
b)-(-3a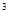 -6a
-6a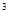 b+3 a
b+3 a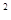 b+10 a
b+10 a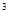 -3)写完后,让王红同学顺便给出一组a、b的值,老师自己说答案,当王红说完:“a=65,b=-2005”后,李老师不假思索,立刻就说出答案“3”。同学们莫名其妙,觉得不可思议,但李老师用坚定的口吻说:“这个答案准确无误”,亲爱的同学你相信吗?你能说出其中的道理吗?
-3)写完后,让王红同学顺便给出一组a、b的值,老师自己说答案,当王红说完:“a=65,b=-2005”后,李老师不假思索,立刻就说出答案“3”。同学们莫名其妙,觉得不可思议,但李老师用坚定的口吻说:“这个答案准确无误”,亲爱的同学你相信吗?你能说出其中的道理吗?查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
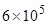 个水龙头,
个水龙头,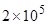 个抽水马桶漏水。如果一个关不紧的水龙头一个月漏掉a立方米水,一个抽水马桶一个月漏掉b立方米水,那么一个月造成的水流失量至少是( )立方米.
个抽水马桶漏水。如果一个关不紧的水龙头一个月漏掉a立方米水,一个抽水马桶一个月漏掉b立方米水,那么一个月造成的水流失量至少是( )立方米.| A.6a+2b | B.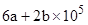 | C.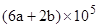 | D.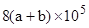 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com