
科目:初中数学 来源:新课标读想用 七年级数学(上)(北师大版) 题型:044
据说,美国著名科学家、避雷针发明者本杰明·富兰克林(1706-1790)逝世时留有若干英镑的遗产,他留下遗嘱说:“……,这××英镑赠给波士顿的居民,如果他们接受了,那么这笔钱应付给一些挑选出来的公民,他们必须把这笔钱按每年5%的利率借给一些年轻的手工业者去生息.过100年后,我希望那时候用100000英镑去建一所公共建筑物,再拿31500英镑去生息……”
根据上述材料,你能算出富兰克林当时留下了多少英镑的遗产吗?(结果保留到整数位)(说明:计算高次方幂可用计算器,例如:(1+2%)100=1.02100,用计算器先按入1.02,再按键,再按入100和等号键,可得结果.)
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江省杭州市江干区九年级上学期期末数学试卷(解析版) 题型:解答题
小明对直角三角形很感兴趣. △ABC中,∠ACB=90°,D是AB上任意一点,连接DC,作DE⊥DC,EA⊥AC,DE与AE交于点E.请你跟着他一起解决下列问题:
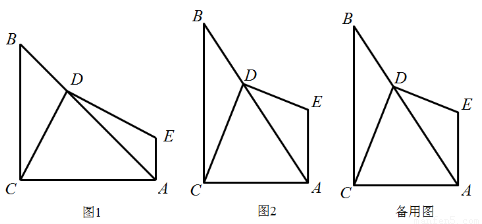
(1)如图1,若△ABC是等腰直角三角形,则DE,DC有什么数量关系?请给出证明.
(2)如果换一个直角三角形,如图2,∠CBA=30°,则DE,DC又有什么数量关系?请给出证明.
(3)由(1)、(2)这两种特殊情况,小明提出问题:如果直角三角形ABC中,BC=mAC,那DE, DC有什么数量关系?请给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
我国著名数学家华罗庚曾说过:“数缺形时少直观,形少数时难入微;数形结合百般好,隔离分家万事休”.数学中,数和形是两个最主要的研究对象,它们之间有着十分密切的联系,在一定条件下,数和形之间可以相互转化,相互渗透.
数形结合的基本思想,就是在研究问题的过程中,注意把数和形结合起来考察,斟酌问题的具体情形,把图形性质的问题转化为数量关系的问题,或者把数量关系的问题转化为图形性质的问题,使复杂问题简单化,抽象问题具体化,化难为易,获得简便易行的成功方案.
例如,求1+2+3+4+…+n的值,其中n是正整数.
对于这个求和问题,如果采用纯代数的方法(首尾两头加),问题虽然可以解决,但在求和过程中,需对n的奇偶性进行讨论.
如果采用数形结合的方法,即用图形的性质来说明数量关系的事实,那就非常的直观.现利用图形的性质来求1+2+3+4+…+n 的值,方案如下:如图,斜线左边的三角形图案是由上到下每层依次分别为1,2,3,…,n个小圆圈排列组成的.而组成整个三角形小圆圈的个数恰为所求式子1+2+3+4+…+n的值.为求式子的值,现把左边三角形倒放于斜线右边,与原三角形组成一个平行四边形.此时,组成平行四边形的小圆圈共有n行,每行有(n+1)个小圆圈,所以组成平行四边形小圆圈的总个数为n(n+1)个,因此,组成一个三角形小圆圈的个数为![]() ,即1+2+3+4+…+n=
,即1+2+3+4+…+n=![]() .
.
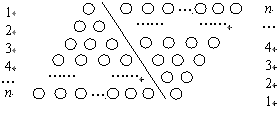
(1)仿照上述数形结合的思想方法,设计相关图形,求1+3+5+7+…+(2n-1)的值,其中 n 是正整数.(要求:画出图形,并利用图形做必要的推理说明)
(2)试设计另外一种图形,求1+3+5+7+…+(2n-1)的值,其中n是正整数.(要求:画出图形,并利用图形做必要的推理说明)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,有两个可以自由转动的均匀转盘A、B,转盘A被均匀地分成4等份,每份分别
标上1、2、3、4四个数字;转盘B被均匀地分成6等份,每份分别标上1、2、3、4、
5、6六个数字.有人为甲、乙两人设计了一个游戏,其规则如下:
⑴同时自由转动转盘A与B;
⑵转盘停止后,指针各指向一个数字(如果指针恰好指在分格线上,那么重转一次,直
到指针停留在某一数字为止),用所指的两个数字作乘积,如果得到的积是偶数,那
么甲胜;如果得到的积是奇数,那么乙胜(如转盘A指针指向3,转盘B指针指向5,3×5
=15,按规则乙胜)。
你认为这样的规则是否公平?请说明理由;如果不公平,请你设计一个公平的规则,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com