
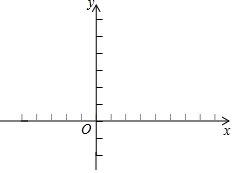 已知抛物线y=ax2+x+c(a≠0)经过点A(-1,0),B(2,0)两点,与y轴相交于点C,点D为抛物线的顶点.
已知抛物线y=ax2+x+c(a≠0)经过点A(-1,0),B(2,0)两点,与y轴相交于点C,点D为抛物线的顶点.分析 (1)把A(-1,0),B(2,0)两点代入抛物线y=ax2+x+c(a≠0)求出a,c的值,再求出其顶点坐标即可;
(2)根据抛物线的对称性可得△ABC的外接圆与抛物线的另一交点E的坐标;
(3)由题意M在线段AB的垂直平分线上,即抛物线对称轴上,设M($\frac{1}{2}$,m),由MC=MA得关于m的方程,解方程即可求解;
(4)作EH⊥AB于H,延长HE至F点使FH=3,则tan∠FBH=3,等量关系可得∠α=∠FBH,∠MPO=∠FBE,作EG⊥FB,△FEG∽△FBH,可得EG=$\frac{\sqrt{10}}{10}$,FG=$\frac{3\sqrt{10}}{10}$,作MN⊥OB于N,在Rt△MPN中,MN=$\frac{1}{2}$,可得NP=$\frac{7}{2}$,进一步可求OP=$\frac{1}{2}$±$\frac{7}{2}$=4或-3.
解答 解:(1)∵抛物线y=ax2+x+c(a≠0)经过A(-1,0),B(2,0)两点,
∴$\left\{\begin{array}{l}{a-1+c=0}\\{4a+2+c=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-1}\\{c=2}\end{array}\right.$.
∴抛物线为y=-x2+x+2=-(x-$\frac{1}{2}$)2+$\frac{9}{4}$,
∴顶点D($\frac{1}{2}$,$\frac{9}{4}$);
(2)E点的坐标为(1,2);
(3)由题意M在线段AB的垂直平分线上,即抛物线对称轴上,
设M($\frac{1}{2}$,m),
由MC=MA得($\frac{3}{2}$)2+m2=($\frac{1}{2}$)2+(2-m)2,
解得m=$\frac{1}{2}$,
∴M($\frac{1}{2}$,$\frac{1}{2}$);
(4)作EH⊥AB于H,延长HE至F点使FH=3,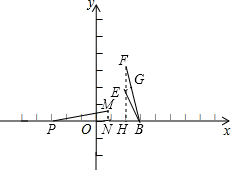 则tan∠FBH=3,
则tan∠FBH=3,
∴∠α=∠FBH,∠MPO=∠FBE,
作EG⊥FB,△FEG∽△FBH,
得EG=$\frac{\sqrt{10}}{10}$,FG=$\frac{3\sqrt{10}}{10}$,
∴BG=$\frac{7\sqrt{10}}{10}$,
∴tan∠FBE=$\frac{1}{7}$,
∴tan∠MPO=$\frac{1}{7}$,
作MN⊥OB于N,在Rt△MPN中,MN=$\frac{1}{2}$,
∴NP=$\frac{7}{2}$,
∴OP=$\frac{1}{2}$±$\frac{7}{2}$=4或-3.
点评 本题考查的是二次函数综合题,涉及到二次函数图象上点的坐标特点、锐角三角函数的定义及相似三角形的判定与性质、勾股定理等知识,难度较大.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题

| A. | x>23 | B. | 23<x≤47 | C. | 11≤x<23 | D. | x≤47 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
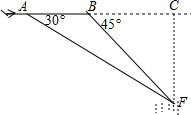 “马航事件”的发生引起了我国政府的高度重视,我国政府迅速派出了舰船和飞机到相关海域进行搜寻.如图,在一次空中搜寻中,水平飞行的飞机在点A处测得前方海面的点F处有疑似飞机残骸的物体(该物体视为静止).此时的俯角为30°,为了便于观察,飞机继续向前飞行了800米到达B点,此时测得点F点俯角为45°.请你计算当飞机飞临F点的正上方点C时(点A、B、C在同一直线上),竖直高度CF约为多少米?(结果保留整数,参考数值:$\sqrt{3}$≈1.7)
“马航事件”的发生引起了我国政府的高度重视,我国政府迅速派出了舰船和飞机到相关海域进行搜寻.如图,在一次空中搜寻中,水平飞行的飞机在点A处测得前方海面的点F处有疑似飞机残骸的物体(该物体视为静止).此时的俯角为30°,为了便于观察,飞机继续向前飞行了800米到达B点,此时测得点F点俯角为45°.请你计算当飞机飞临F点的正上方点C时(点A、B、C在同一直线上),竖直高度CF约为多少米?(结果保留整数,参考数值:$\sqrt{3}$≈1.7)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在?ABCD中,CE平分∠BCD,交AD于点E,DF平分∠ADC,交BC于点F,CE与DF交于点P,连接EF,BP.
如图,在?ABCD中,CE平分∠BCD,交AD于点E,DF平分∠ADC,交BC于点F,CE与DF交于点P,连接EF,BP.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
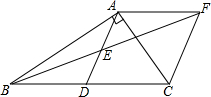 在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com