
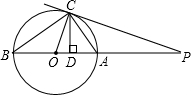
 如图,点P是⊙O的直径BA延长线上一点,PC与⊙O相切于点C,CD⊥AB,垂足为D,连接AC、BC、OC,那么下列结论中:①PC2=PA•PB;②PC•OC=OP•CD;③OA2=OD•OP;④CD2>BD•AD,正确的有①②③.
如图,点P是⊙O的直径BA延长线上一点,PC与⊙O相切于点C,CD⊥AB,垂足为D,连接AC、BC、OC,那么下列结论中:①PC2=PA•PB;②PC•OC=OP•CD;③OA2=OD•OP;④CD2>BD•AD,正确的有①②③. 分析 ①证明△PBC∽△PCA,即可得到结论,这实际上是圆的切割线定理,正确;
②根据切线的性质定理,得OC⊥PC,求出△OCD∽△OPC,得出比例式即可,正确;
③根据相似三角形的性质得出比例式,即可得出答案,正确;
④证△BDC∽△CDA,即可得出答案,错误.
解答 解:①∵PC与⊙O相切于点C,
∴∠PCB=∠A,∠P=∠P,
∴△PBC∽△PCA,
∴PC2=PA•PB;
②∵OC⊥PC,PC切⊙O于C,
∴∠PCO=∠CDO=90°,
∵∠COD=∠POC,
∴△OCD∽△OPC,
∴$\frac{PC}{CD}$=$\frac{OC}{OP}$,
∴PC•OC=OP•CD;
③∵△OCD∽△OPC,
∴$\frac{OC}{OD}$=$\frac{OP}{OC}$,
∴OC2=OD•OP,
∵OA=OC,
∴OA2=OD•OP;
④∵AB为直径,
∴∠BCA=90°,
∵CD⊥AB,
∴∠BDC=∠ADC=90°,
∴∠B+∠BCD=∠BCD+∠ACD=90°,
∴∠B=∠ACD,
∴△BDC∽△CDA,
∴$\frac{CD}{AD}$=$\frac{BD}{CD}$,
∴CD2=BD•AD,
∴①②③正确;④错误;
故答案为:①②③.
点评 本题考查了切线的性质,相似三角形的性质和判定的应用,能灵活运用定理进行推理是解此题的关键,注意:圆的切线垂直于过切点的半径.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:初中数学 来源: 题型:选择题
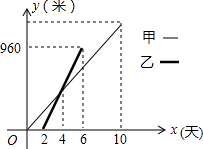 今年3月,市路桥公司决定对A、B两地之间的公路进行改造,并由甲工程队从A地向B地方向修筑,乙工程队从B地向A第方向修筑.已知甲工程队先施工2天,乙工程队再开始施工,乙工程队施工几天后因另有任务提前离开,余下的任务由甲工程队单独完成,直到公路修通.甲、乙两个工程队修公路的长度y(米)与施工时间x(天)之间的函数关系如图所示.下列说法:
今年3月,市路桥公司决定对A、B两地之间的公路进行改造,并由甲工程队从A地向B地方向修筑,乙工程队从B地向A第方向修筑.已知甲工程队先施工2天,乙工程队再开始施工,乙工程队施工几天后因另有任务提前离开,余下的任务由甲工程队单独完成,直到公路修通.甲、乙两个工程队修公路的长度y(米)与施工时间x(天)之间的函数关系如图所示.下列说法:| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
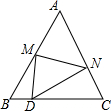 如图,等边△ABC中,D是边BC上的一点,且BD:DC=1:3,把△ABC折叠,使点A落在边BC上的点D处,那么$\frac{△BMD的面积}{△CDN的面积}$的值为$\frac{25}{49}$.
如图,等边△ABC中,D是边BC上的一点,且BD:DC=1:3,把△ABC折叠,使点A落在边BC上的点D处,那么$\frac{△BMD的面积}{△CDN的面积}$的值为$\frac{25}{49}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
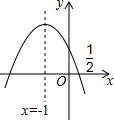 如图,抛物线y=ax2+bx+c(a≠0)的对称轴是x=-1,且过点($\frac{1}{2}$,0),有下列结论:①abc>0;②a-2b+4c=0;③25a-10b+4c=0;④3b+2c>0.其中所有正确的结论是①③(填写序号)
如图,抛物线y=ax2+bx+c(a≠0)的对称轴是x=-1,且过点($\frac{1}{2}$,0),有下列结论:①abc>0;②a-2b+4c=0;③25a-10b+4c=0;④3b+2c>0.其中所有正确的结论是①③(填写序号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com