
 将图中的△ABC作如下运动:
将图中的△ABC作如下运动:分析 (1)利用点平移的坐标规律写出点A1,C1,B1的坐标,然后描点即可;
(2)延长AB到B2使AB2=2AB,延长AC到C2使AC2=2AB,则可得到△AB2C2,然后写出点B2、C2两个顶点的坐标.
解答 解:(1)如图,△A1B1C1为所作,A1(-1,0),C1(-2,1),B1(1,2);
(2)如图,△AB2C2为所作,点B2、C2两个顶点的坐标分别为(4,4),(-1,2).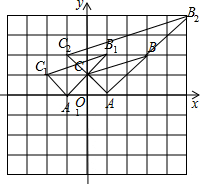
点评 本题考查了作图-位似变换:画位似图形的一般步骤为:先确定位似中心;再分别连接并延长位似中心和能代表原图的关键点;接着根据位似比,确定能代表所作的位似图形的关键点;然后顺次连接上述各点,得到放大或缩小的图形.也考查了平移变换.


科目:初中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
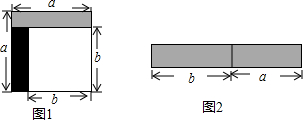 从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
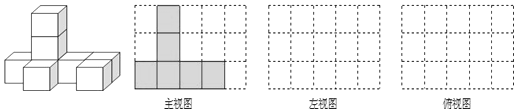
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平面直角坐标系xOy中,直线y=$\frac{3}{2}$x与双曲线y=$\frac{6}{x}$相交于A,B两点,C是第一象限内双曲线上一点,连接CA并延长交y轴于点P,连接BP,BC.若△PBC的面积是20,则点C的坐标为( )
如图,在平面直角坐标系xOy中,直线y=$\frac{3}{2}$x与双曲线y=$\frac{6}{x}$相交于A,B两点,C是第一象限内双曲线上一点,连接CA并延长交y轴于点P,连接BP,BC.若△PBC的面积是20,则点C的坐标为( )| A. | ($\frac{14}{3}$,$\frac{9}{7}$) | B. | (4,$\frac{3}{2}$) | C. | (5,$\frac{6}{5}$) | D. | ($\frac{16}{3}$,$\frac{9}{8}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一次函数y=kx+b与反比例函数$y=\frac{m}{x}$的图象交于A(2,3),B(-3,n)两点.
如图,一次函数y=kx+b与反比例函数$y=\frac{m}{x}$的图象交于A(2,3),B(-3,n)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,将△ABC绕点A逆时针旋转90°后得到△A′C′.
每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,将△ABC绕点A逆时针旋转90°后得到△A′C′.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com