
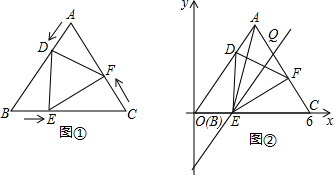
分析 (1)由三角形ABC为等边三角形,以及AD=BE=CF,进而得出三角形ADF与三角形CFE与三角形BED全等,利用全等三角形对应边相等得到BF=DF=DE,即可得证;
(2)作DG⊥BC于G,AH⊥BC于H,表示出AH与DG,进而表示出三角形ABC与三角形BED面积,由三角形ABC面积减去3个三角形BED面积表示出y与t的函数解析式,利用二次函数性质求出y的最小值,以及此时t的值;
(3)由(2)表示出三角形AEC面积,根据EQ与AB平行,得到三角形CEQ与三角形ABC相似,利用相似三角形面积比等于相似比的平方表示出三角形CEQ面积,进而表示出AEQ面积,利用二次函数的性质求出面积最大值,并求出此时Q的坐标即可.
解答  (1)证明:在等边三角形ABC中,AB=BC=AC=6,∠A=∠B=∠C=60°,
(1)证明:在等边三角形ABC中,AB=BC=AC=6,∠A=∠B=∠C=60°,
由题意知,当0<t<6时,AD=BE=CF=t,
∴BD=CE=AF=6-t,
∴△ADF≌△CFE≌△BED(SAS),
∴EF=DF=DE,
∴△DEF是等边三角形,
∴不论t如何变化,△DEF始终为等边三角形;
(2)解:作DG⊥BC于G,AH⊥BC于H,则AH=AB•sin60°=3$\sqrt{3}$,DG=BD•sin60°=$\frac{\sqrt{3}(6-t)}{2}$,
∴S△ABC=$\frac{1}{2}$×6×3$\sqrt{3}$=9$\sqrt{3}$,S△BED=$\frac{1}{2}$BE•DG=$\frac{1}{2}$t•$\frac{\sqrt{3}(6-t)}{2}$=$\frac{\sqrt{3}t(6-t)}{4}$,
由(1)知△ADF≌△CFE≌△BED,
∴y=S△ABC-3S△BED=9$\sqrt{3}$-$\frac{3\sqrt{3}t(6-t)}{4}$=$\frac{3\sqrt{3}}{4}$t2-$\frac{9\sqrt{3}}{2}$t+9$\sqrt{3}$=$\frac{3\sqrt{3}}{4}$(t-3)2+$\frac{9\sqrt{3}}{4}$,
∵a=$\frac{3\sqrt{3}}{4}$>0,∴抛物线开口向上,有最小值,
∴当t=3时,y最小,y最小=$\frac{{9\sqrt{3}}}{4}$cm2.
(3)解:由(2)知,AH=3$\sqrt{3}$,
∴S△AEC=$\frac{1}{2}$×3$\sqrt{3}$×(6-t)=$\frac{3\sqrt{3}(6-t)}{2}$,
∵EQ∥AB,
∴△CEQ∽△ABC,
∴$\frac{{S}_{△CEQ}}{{S}_{△ABC}}$=($\frac{CE}{CB}$)2=$\frac{(6-t)^{2}}{36}$,即S△CEQ=$\frac{(6-t)^{2}}{36}$S△ABC=$\frac{(6-t)^{2}}{36}$×9$\sqrt{3}$=$\frac{\sqrt{3}(6-t)^{2}}{4}$,
∴S△AEQ=S△AEC-S△CEQ=$\frac{3\sqrt{3}(6-t)}{2}$-$\frac{\sqrt{3}(6-t)^{2}}{4}$=-$\frac{\sqrt{3}}{4}$(t-3)2+$\frac{9\sqrt{3}}{4}$,
∵a=-$\frac{\sqrt{3}}{4}$<0,
∴抛物线开口向下,有最大值,
∴当t=3时,△AEQ的面积最大为$\frac{{9\sqrt{3}}}{4}$cm2,
此时E点为BC的中点,线段EQ为△ABC的中位线,作QK⊥BC于K,如图,
∴EQ=$\frac{1}{2}$AB=3,
在Rt△EQK中,∠QEK=60°,
∴QK=EQ•sin60°=$\frac{3\sqrt{3}}{2}$,EK=EQ•cos60°=$\frac{3}{2}$,即BK=BE+EK=3+$\frac{3}{2}$=$\frac{9}{2}$,
∴Q坐标为($\frac{9}{2}$,$\frac{3\sqrt{3}}{2}$).
点评 此题考查了相似形综合题,涉及的知识有:等边三角形的判定与性质,坐标与图形性质,二次函数的性质,相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解本题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
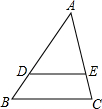 如图,△ABC中,点D、E分别在AB、AC边上,DE∥BC,若AD:AB=3:4,△ABC的面积为
如图,△ABC中,点D、E分别在AB、AC边上,DE∥BC,若AD:AB=3:4,△ABC的面积为| A. | 9 | B. | 12 | C. | 4 | D. | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,矩形纸片ABCD中,AB=5cm,点E在BC上,且AE=EC.若将纸片沿AE折叠,点B恰好与AC上的点B′重合,则AC=10 cm.
如图所示,矩形纸片ABCD中,AB=5cm,点E在BC上,且AE=EC.若将纸片沿AE折叠,点B恰好与AC上的点B′重合,则AC=10 cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com