
【题目】如图,在矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,则AP的长为 ( ) .

A.4.8B.3![]() C.5D.3
C.5D.3![]()
【答案】A
【解析】
由折叠的性质得出EP=AP,∠E=∠A=90°,BE=AB=8,由ASA证明△ODP≌△OEG,得出OP=OG,PD=GE,设AP=EP=x,则PD=GE=6x,DG=x,求出CG、BG,根据勾股定理得出方程,解方程即可.
解:如图所示,设BE与CD交于点G,

∵四边形ABCD是矩形,
∴∠D=∠A=∠C=90°,AD=BC=6,CD=AB=8,
根据题意得:△ABP≌△EBP,
∴EP=AP,∠E=∠A=90°,BE=AB=8,
在△ODP和△OEG中,
∠D=∠E,OD=OE,∠DOP=∠EOG,
∴△ODP≌△OEG(ASA),
∴OP=OG,PD=GE,
∴DG=EP,
设AP=EP=x,则PD=GE=6x,DG=x,
∴CG=8x,BG=8(6x)=2+x,
根据勾股定理得:BC2+CG2=BG2,
即62+(8x)2=(x+2)2,
解得:x=4.8,
∴AP=4.8,
故选:A.


科目:初中数学 来源: 题型:
【题目】如图,∠AGF=∠ABC,∠1+∠2=180°.
(1)试判断BF与DE的位置关系,并说明理由;
(2)若BF⊥AC,∠2=150°,求∠AFG的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,BD与CE相交于点O,AD=AE,∠B=∠C,请解答下列问题:
(1)△ABD与△ACE全等吗?为什么?
(2)BO与CO相等吗?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
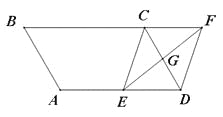
【题目】(7分)如图,平行四边形ABCD中,AB=3cm,BC=5cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
(1)求证:四边形CEDF是平行四边形;
(2)①当AE= cm时,四边形CEDF是矩形;
②当AE= cm时,四边形CEDF是菱形;(直接写出答案,不需要说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一块长16m,宽12m的矩形荒地上建造一个花园,要求花轩占地面积为荒地面积的一半,下面分别是小强和小颖的设计方案.
(1)你认为小强的结果对吗?请说明理由.

(2)请你帮助小颖求出图中的x.
(3)你还有其他的设计方案吗?请在图(3)中画出一个与图(1)(2)有共同特点的设计草图,并加以说明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),矩形OABC的边OA、OC在坐标轴上,点B坐标为(5,4),点P是射线BA上的一动点,把矩形OABC沿着CP折叠,点B落在点D处.
(1)当点C、D、A共线时,AD= ;
(2)如图(2),当点P与点A重合时,CD与x轴交于点E,过点E作EF⊥AC,交BC于点F,请判断四边形AECF的形状,并说明理由;
(3)若点D正好落在x轴上,请直接写出点P的坐标: .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了让学生能更加了解温州历史,某校组织七年级师生共480人参观温州博物馆.学校向租车公司租赁A、B两种车型接送师生往返,若租用A型车3辆,B型车6辆,则空余15个座位;若租用A型车5辆,B型车4辆,则15人没座位.
(1)求A、B两种车型各有多少个座位;
(2)若A型车日租金为350元,B型车日租金为400元,且租车公司最多能提供7辆B型车,应怎样租车能使座位恰好坐满且租金最少,并求出最少租金.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com