
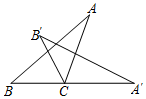
 如图,将△ABC绕点C按顺时针方向旋转64°至△A′B′C,使点A′落在BC的延长线上.则∠ACB′=52度.
如图,将△ABC绕点C按顺时针方向旋转64°至△A′B′C,使点A′落在BC的延长线上.则∠ACB′=52度. 科目:初中数学 来源: 题型:解答题
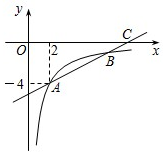 如图,已知一次函数y=kx+b的图象与反比例函数y=$\frac{4-2m}{x}$(x>0)的图象交于点A(2,-4)和点B,与x轴交于点C,且$\frac{BC}{AB}$=$\frac{1}{3}$.
如图,已知一次函数y=kx+b的图象与反比例函数y=$\frac{4-2m}{x}$(x>0)的图象交于点A(2,-4)和点B,与x轴交于点C,且$\frac{BC}{AB}$=$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
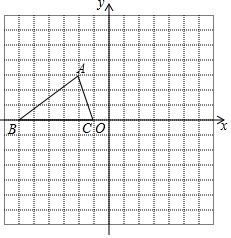 已知,如图所示的正方形网格中,每个网格的单位长度为1,△ABC的顶点均在格点上,根据所给的平面直角坐标系解答下列问题:
已知,如图所示的正方形网格中,每个网格的单位长度为1,△ABC的顶点均在格点上,根据所给的平面直角坐标系解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
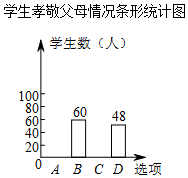 某校为了了解学生孝敬父母的情况(选项:A.为父母洗一次脚;B.帮父母做一次家务;C.给父母买一件礼物;D.其它),在全校范围内随机抽取了若干名学生进行调查,得到如图表(部分信息未给出):根据以上信息解答下列问题:
某校为了了解学生孝敬父母的情况(选项:A.为父母洗一次脚;B.帮父母做一次家务;C.给父母买一件礼物;D.其它),在全校范围内随机抽取了若干名学生进行调查,得到如图表(部分信息未给出):根据以上信息解答下列问题:| 选项 | 频数 | 频率 |
| A | m | 0.15 |
| B | 60 | p |
| C | n | 0.4 |
| D | 48 | 0.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
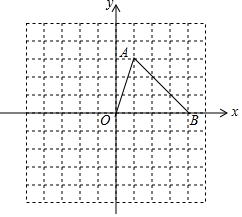 如图,在平面直角坐标系中,△ABO的三个顶点坐标分别为A(1,3),B(4,0),O(0,0).
如图,在平面直角坐标系中,△ABO的三个顶点坐标分别为A(1,3),B(4,0),O(0,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com