
【题目】如图,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2﹣10ax+16a(a≠0)交x轴于A、B两点,抛物线的顶点为D,对称轴与x轴交于点H,且AB=2DH.
(1)求a的值;
(2)点P是对称轴右侧抛物线上的点,连接PD,PQ⊥x轴于点Q,点N是线段PQ上的点,过点N作NF⊥DH于点F,NE⊥PD交直线DH于点E,求线段EF的长;
(3)在(2)的条件下,连接DN、DQ、PB,当DN=2QN(NQ>3),2∠NDQ+∠DNQ=90°时,作NC⊥PB交对称轴左侧的抛物线于点C,求点C的坐标.
【答案】
(1)
解:令y=0,
∵a≠0,
∴x2﹣10x+16=0,得x=2或x=8,
∴点A(2,0),B(8,0),
∴AB=8﹣2=6,
∵AB=2DH,
∴DH=3,
∵OH=2+ ![]() ,
,
∴D(5,﹣3),
∴﹣3=a×52﹣10a×5+16a,得a= ![]()
(2)
解:如图1,过点D作PQ的垂线,交PQ的延长线于点M,
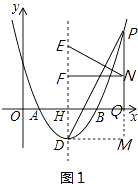
∵NE⊥PD,
∴∠DPN+∠PNE=90°,
∵NF⊥DE,
∴∠FEN+∠FNE=90°,
又∵DH⊥x轴,PQ⊥x轴,
∴DE∥PQ,
∴∠FEN=∠PNE,
∴∠DPM=∠ENF,
∴△EFN∽△DMP,
∴ ![]() ,
,
设点P(t, ![]() ),
),
则FN=DM=t﹣5,PM= ![]() +3,
+3,
∴ ![]() ,
,
解得,EF=3
(3)
解:如图2,作QG⊥DN于点G,
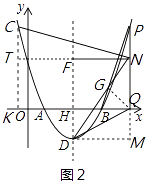
∵DF∥PQ,
∴∠FDN=∠DNQ,
∵2∠NDQ+∠DNQ=90°,
∴2∠NDQ+∠FDN=90°,
∵∠FDM=90°,
∴∠NDM=2∠NDQ,
∴∠NDQ=∠MDQ,
∴QG=QM=DH=3,
设QN=m,则DN=2m,
∵sin∠DNM= ![]() ,sin∠QNG=
,sin∠QNG= ![]() ,sin∠DNM=sin∠QNG,
,sin∠DNM=sin∠QNG,
∴ ![]() ,得DM=6=DG,
,得DM=6=DG,
∴OQ=5+6=11,
∴点P的纵坐标是: ![]() ,
,
∴点P(11,9),
∵NG=DN﹣DG=2m﹣6,在Rt△NGQ中,QG2+NG2=QN2,
∴32+(2m﹣6)2=m2,
解得,m=3(舍去)或m=5,
设点C的坐标为(n, ![]() ),作CK⊥x轴于点K,作NF⊥CK于点K,
),作CK⊥x轴于点K,作NF⊥CK于点K,
则CT= ![]() ,NT=11﹣n,
,NT=11﹣n,
∵P(11,9),则BQ=11﹣8=3,PQ=9,
∵CN⊥PB,PQ∥CK,PQ⊥x轴,
∴△CTN∽△BQP,
∴ ![]() ,
,
即 ![]() ,
,
解得,n=﹣1或n=10(舍去),
∴点C(﹣1,9).
【解析】(1)根据y=ax2﹣10ax+16a可以求得当y=0时,x的值,从而可以求得点A、B的坐标,由抛物线的顶点为D,对称轴与x轴交于点H,且AB=2DH,从而可以求得a的值;(2)根据已知条件作出相应的图形,然后根据题意题目中的数量关系,通过灵活变形可以求得EF的长;(3)根据题意可以画出相应的图形,然后根据题目中的关系,利用三角形相似,灵活变化可以求得点C的坐标.
【考点精析】利用二次函数的图象和二次函数的性质对题目进行判断即可得到答案,需要熟知二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


科目:初中数学 来源: 题型:
【题目】如图,在方格纸中,A,B,C三点都在小方格的顶点上(每个小方格的边长为1). 
(1)在图甲中画一个以A,B,C为其中三个顶点的平行四边形,并求出它的周长. 
(2)在图乙中画一个经过A,B,C三点的圆,并求出圆的面积. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知点A(﹣1,0),B(﹣1,1),C(1,0),D(1,2),点P是坐标系内一点,给出定义:若存在过点P的直线l与线段AB,CD都有公共点,则称点P是线段AB,CD的“联络点”.现有点P(x,y)在直线y= ![]() x上,且它是线段AB,CD的“联络点”,则x的取值范围是 .
x上,且它是线段AB,CD的“联络点”,则x的取值范围是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李老师为了了解所教班级学生完成数学课前预习的具体情况,对本班部分学生进行了为期半个月的跟踪调查,他将调查结果分为四类,A:很好;B:较好;C:一般;D:较差.并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题: 
(1)李老师一共调查了多少名同学?
(2)C类女生有3名,D类男生有1名,将图1条形统计图补充完整;
(3)为了共同进步,李老师想从被调查的A类和D类学生中各随机选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车到达A处,返程时从A处乘坐升降电梯直接到达C处,已知:AC⊥BC于C,DE∥BC,AC=200.4米,BD=100米,∠α=30°,∠β=70°,则AE的长度约为米.(参考数据:sin70≈0.94,cos70°≈0.34,tan70°≈2.25). 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解一路段车辆行驶速度的情况,交警统计了该路段上午7::0至9:00来往车辆的车速(单位:千米/时),并绘制成如图所示的条形统计图.这些车速的众数、中位数分别是( ) 
A.众数是80千米/时,中位数是60千米/时
B.众数是70千米/时,中位数是70千米/时
C.众数是60千米/时,中位数是60千米/时
D.众数是70千米/时,中位数是60千米/时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明到服装店进行社会实践活动,服装店经理让小明帮助解决以下问题:服装店准备购进甲乙两种服装,甲种每件进价80元,售价120元,乙种每件进价60元,售价90元.计划购进两种服装共100件,其中甲种服装不少于65件.
(1)若购进这100件服装的费用不得超过7500元,则甲种服装最多购进多少件??
(2)在(1)的条件下,该服装店对甲种服装以每件优惠a(0<a<20)元的价格进行促销活动,乙种服装价格不变,那么该服装店应如何调整进货方案才能获得最大利润?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com