
����Ŀ���۲�������������
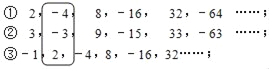
ȡÿһ�еĵ�n���������μ�Ϊx��y��z������ͼ�У���n=2ʱ��x=��4��y=��3��z=2��
��1����n=7ʱ����ֱ��д��x��y��z��ֵ��������������������������С�����IJ
��2����֪nΪż������x��y��z��������������������С�����IJ�Ϊ384����n��ֵ��
��3����m=x+y+z����x��y��z��������������������С�����IJ�Ϊ�� �����ú�m��ʽ�ӱ�ʾ��
���𰸡���1��x=128��y=129��z=��64��������������������С�����IJ�Ϊ193����2��n=8����3����nΪ����ʱ��Ϊm����nΪż��ʱ��Ϊ1��m��
��������
��1��������֪���֣������е������ӵڶ�������ʼ������һ������ǰ��һ�����˩�2�õ��ģ������е��������ж�Ӧ������1�������е���Ϊ�����ж�Ӧ������һ����෴�������˷ֱ����x��y��z��ֵ��������⼴�ɣ�
��2�������жϳ�nΪż��ʱ��z���x��С�������z��x=��![]() x��x=��
x��x=��![]() x������x��y��z��������������������С�����IJ�Ϊ384�г����̣��������n��ֵ��
x������x��y��z��������������������С�����IJ�Ϊ384�г����̣��������n��ֵ��
��3������m=x+y+z���m=��![]() ������2��n+1���ٷ�nΪ������nΪż������������ۼ��ɣ�
������2��n+1���ٷ�nΪ������nΪż������������ۼ��ɣ�
��1���������⣬��x=������2��7=128��y=������2��7+1=129��z=��![]() ��[������2��7]=��64��
��[������2��7]=��64��
��������������������С�����IJ�Ϊ��129������64��=193��
��2����nΪż��ʱ��x��y��0��z��0��
��z=��![]() x��
x��
��z��x=��![]() x��x=��
x��x=��![]() x=384��
x=384��
��x=��256��
�ߩ�����2��8=��256��
��n=8��
��3��m=x+y+z=������2��n+[������2��n+1]+{��![]() ��[������2��n]}
��[������2��n]}
=������2��n������2��n+1+![]() ������2��n
������2��n
=��![]() ������2��n+1��
������2��n+1��
����nΪ����ʱ��y��x��z��
y��z=[������2��n+1]��{��![]() ��[������2��n]}
��[������2��n]}
=������2��n+1��![]() ������2��n
������2��n
=��![]() ������2��n+1
������2��n+1
=m��
����nΪż��ʱ��z��y��x��
z��x={��![]() ��[������2��n]}��[������2��n]
��[������2��n]}��[������2��n]
=![]() ������2��n+����2��n
������2��n+����2��n
=![]() ������2��n
������2��n
=1��m��
�ʴ�Ϊ��nΪ����ʱ��Ϊm����nΪż��ʱ��Ϊ1��m��


 ��ѧȫ��������ѵ��ϵ�д�
��ѧȫ��������ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
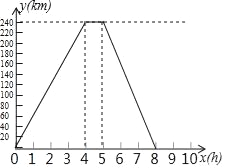
����Ŀ��һ��������A���˻���240km��B�أ�ж����A�أ���ͼ��ʵ���ǻ�����A�ص�·��y��km�����ڳ������ʱ��x��h��֮��ĺ���ͼ��������ʱ������һ�����г���������AB֮�䣬��A��40km������ÿСʱ20km���ٶȱ���B�أ�
��1������ȥB�ص��ٶ����� ����ж�������� ��Сʱ�����ص��ٶ����� ����
��2��������г������ž�A�ص�·��y��km������x�ĺ�����ϵʽ�����ڴ�����ϵ�л�������ͼ��
��3�������г������������ӭ���������ǻ���������Сʱ�����г������Ż��ж�Զ����B�أ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪��1+2+3+��+![]() =
=![]() ����1+2+3+��+10�� ___________ .
����1+2+3+��+10�� ___________ .
[�������] ��ô ![]() �Ľ�����ڶ����أ�
�Ľ�����ڶ����أ�
[�Ķ�����] ��ͼ1��ʾ�������������У���1��ԲȦ�е���Ϊ1����12 ����2������ԲȦ�����ĺ�Ϊ2+2����22��......����n��n��ԲȦ�����ĺ�Ϊn+n+![]() n�� n2���������������������й���____ ��ԲȦ������ԲȦ�����ĺͿɱ�ʾΪ_________________ .
n�� n2���������������������й���____ ��ԲȦ������ԲȦ�����ĺͿɱ�ʾΪ_________________ .
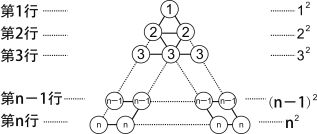
ͼ1
[����̽��] ������������������ת�ɵ���ͼ2��ʾ�����������۲��������������������ͬһλ��ԲȦ�е��������n��1�еĵ�һ��ԲȦ�е����ֱ�Ϊn��1��2��n������ÿ��λ��������ԲȦ�е����ĺ;�Ϊ______________.�ɴ˿ɵã���������������������ԲȦ�������ܺ�Ϊ��
3��![]() ����_________________.��ˣ�
����_________________.��ˣ�![]() ��__________.
��__________.

ͼ2
[������]
��1��.�������Ϲ��ɿɵ�![]() __________________.
__________________.
��2��.�Լ��� ![]() ����д�����㲽��.
����д�����㲽��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ������װ�ã�������ֵΪxʱ�������ֵΪy����y��x�Ķ��κ�������֪����ֵΪ��2��0��1ʱ����Ӧ�����ֵ�ֱ�Ϊ5����3����4�� 
��1����˶��κ����Ľ���ʽ��
��2��������������ϵ�л���������κ�����ͼ������ͼ��д�������ֵyΪ����ʱ����ֵx��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������A�س�������һ����������Ľֵ���������ÿ����ʻ�����������Ϊ������¼���£�x��5��x��14����λ��m����
��ʻ���� | ��һ�� | �ڶ��� | ������ | ���Ĵ� |
��ʻ��� | x | �� | x��3 | 2��5��x�� |
��ʻ���������������������� | �� �� | �� �� | �� �� | �� �� |
��1���뽫����������
��2��������4����ʻ������������ڵ�λ�ã�
��3���������ʻ����·��Ϊ41m�����һ����ʻ��·��x��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���C=90�㣬AC=4��BC=3������ABC�Ƶ�A��ʱ����ת��ʹ��C�����߶�AB�ϵĵ�E������B���ڵ�D������B��D�����ľ���Ϊ �� 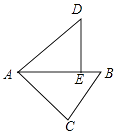
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�ų�����ֽ���ϻ�һ�����ᣮ

��1�����۵�ֽ���������ϱ�ʾ��3�ĵ����ʾ5�ĵ��غϣ����ۺ�������Ľ����ʾ����Ϊ�� ����
��2��������ֽ����ͼ�����ߴ����������м��һ��ֽ�����ۣ�ʹ�����������غϣ�������������2�κ��ٽ���չ����������˵��ۺۺ����Ҷ˵��ۺ�������Ľ����ʾ�����ֱ����� ����
��3������������ϵ��������ʾ����Ϊa��b���������ۣ�����ǡ���غϣ����ۺ�������Ľ����ʾ����Ϊ�� �������ú�a��b�Ĵ���ʽ��ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB��90��������C��ֱ��MN��AB��DΪAB����һ�㣬����D��DE��BC����ֱ��MN��E������ΪF������CD��BE.
��1����֤��CE��AD��
��2����DΪAB�е�ʱ���ı���BECD��ʲô�����ı��Σ�˵��������ɣ�
��3����DΪAB�е㣬��A�Ĵ�С����ʲô����ʱ���ı���BECD�������Σ���˵��������ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��P�ǵȱߡ�ABC�ڲ�һ�㣬��APB����BPC����CPA�Ĵ�С֮����5��6��7������ABP��ʱ����ת��ʹ��AB��AC�غϣ�����PA��PB��PC�ij�Ϊ�ߵ������ε������ǡ�PCQ����QPC����PQC= �� 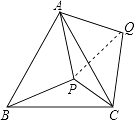
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com